Previously we showed that morphisms locally of finite type are preserved under base change. We can use this to show that

Given a morphism of schemes , the preimage of any affine can be covered by affines such that the corresponding ring maps are of finite type.

Alternatively, if we define a morphism locally of finite type to be one that satisfies , then what we are saying is that such a property can be checked on a cover; we can replace “any affine” with “an affine in a cover of affines”.

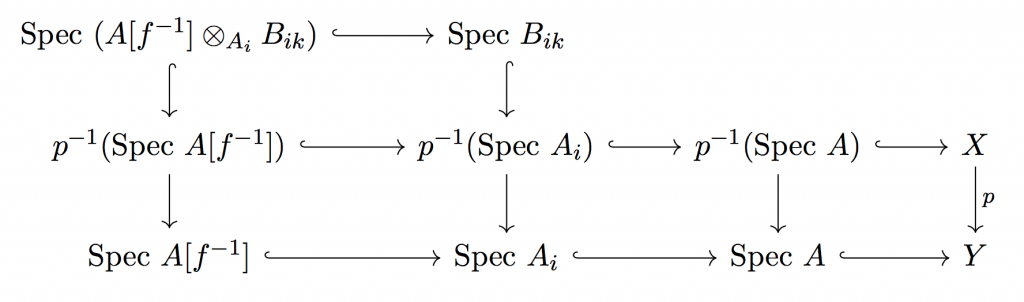
Let’s try to prove . First, we base change to . Since the morphism is also locally of finite type, we can cover by affines such that their preimages can be covered by the spectra of finitely-generated -algebras . However, we don’t know if these are finitely-generated -algebras! To fix this, we base change to even smaller affines. Cover by basic open sets . This gives us a cover of each by basic open sets of the form . Since is of finite type, is of finite type. Since is clearly of finite type, is of finite type, giving us the desired cover of . The following diagram may be illustrative (every square is a pullback)