Author |
Topic: Linear Algebra ---- eigenvalues/eigenvectors (Read 3291 times) |
|
MonicaMath
Newbie
Gender: 
Posts: 43
|
 |
Linear Algebra ---- eigenvalues/eigenvectors
« on: Mar 3rd, 2009, 3:00pm » |
 Quote  Modify
|
hi,,
could anyone help me !!
What is the relation between the eigenvalues of the matrix A and thos for the matrix B, where
A= [ b a+c 0 0
a b a+c 0
0 a b a+c
0 0 a b ]
and
B =[ d e 0 0
e d e 0
0 e d e
0 0 e d ]
with d ,e are related to a, b , and c.
These are both tridiagonal matrices.
So Im trying to find the eigenvalues and eigenvectors of a nonsymmetric tridiagonal matrix A by finding the eigenvalues and eigenvectors of a symmetric tridiagonal matrix B, with some relation between d,e and b,a,and c .
so, what u suggest ??
|
|
 IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender: 
Posts: 1948
|
|
Re: Linear Algebra ---- eigenvalues/eigenvectors
« Reply #1 on: Mar 4th, 2009, 1:08am » |
Quote Modify
|
Please don't post the same problem to multiple forums.
The idea is probably that for any a,b,c, you can find d,e such that B is similar to A.
If this is the case, you need tr A = tr B and det A = det B. This gives you two equations to relate a,b,c with d,e. Under these conditions, it turns out A and B actually are similar (assuming e 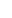 0). In fact, show that there is a diagonal matrix D such that AD=DB.
|
| « Last Edit: Mar 4th, 2009, 1:11am by Eigenray » |
IP Logged |
|
|
|
MonicaMath
Newbie
Gender:
Posts: 43
|
|
Re: Linear Algebra ---- eigenvalues/eigenvectors
« Reply #2 on: Mar 4th, 2009, 12:54pm » |
Quote Modify
|
HI,
Thank you for your replay,
I solved the problem, and both A and B have the same eigenvalues, but the eigevectore differ !
my solution is as follows,
d will be: d =b - 2a,
and: e=sqrt(a^2 + ac ),
A and B have the same trace and same determinant, but there still some wrong ??
( take as an example a=2, b=3, c=-7
so d=3, and e=sqrt(-5) )
so what is my mistake ??
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Linear Algebra ---- eigenvalues/eigenvectors
« Reply #3 on: Mar 4th, 2009, 1:47pm » |
Quote Modify
|
on Mar 4th, 2009, 12:54pm, MonicaMath wrote:Correct me if I'm wrong, but isn't the trace the sum of the elements on the diagonal? And therefore since we have 4 times b on the diagonal in A, and 4 times d on the diagonal in B, we must have d=b.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Linear Algebra ---- eigenvalues/eigenvectors
« Reply #4 on: Mar 4th, 2009, 1:56pm » |
Quote Modify
|
If A and B are similar there will be an isomorphism that takes the eigenvectors of one to the eigenvectors of the other. That is, suppose B = P-1AP. Then v is an eigenvector of B if and only if Pv is an eigenvector of A (with the same eigenvalue).
|
|
IP Logged |
|
|
|
MonicaMath
Newbie
Gender:
Posts: 43
|
|
Re: Linear Algebra ---- eigenvalues/eigenvectors
« Reply #5 on: Mar 4th, 2009, 2:06pm » |
Quote Modify
|
Sorry for my misstype ..
d= - c - 2a , (not b - 2a)
and e is still the same.
|
|
IP Logged |
|
|
|
MonicaMath
Newbie
Gender:
Posts: 43
|
|
Re: Linear Algebra ---- eigenvalues/eigenvectors
« Reply #6 on: Mar 4th, 2009, 2:09pm » |
Quote Modify
|
Thanks Mr. Eigenray ,,,
you are right .... but how I can fine a formula for that matrix P ?
if you can help me then my problem will be solved ...
thanks
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Linear Algebra ---- eigenvalues/eigenvectors
« Reply #7 on: Mar 4th, 2009, 2:15pm » |
Quote Modify
|
The relation should be d = b, e2 = a(a+c). As a hint, it turns out you can take P to be a diagonal matrix. Since any scalar multiple of P will also work, you can assume the upper-left entry is a 1. Then there are only three variables you should be able to solve for to get AP = PB.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print