Author |
Topic: Barometric equation for a mixture of two gasses (Read 2855 times) |
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Barometric equation for a mixture of two gasses
« on: Sep 24th, 2007, 1:59pm » |
 Quote  Modify
|
I'm trying to work out the barometric equation for a mixture of 20% oxygen and 80% nitrogen at 10km altitude (assuming constant temperature of 273K, and 1 bar at ground level)
(And yes it's homework, although I doubt I'm expected to go beyond what I already did)
It's easy to reason that the sum of the partial pressures has to satisfy
pO2(h) + pN2(h) =  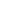 h [MO2(h) pO2(h) + MN2(h) pN2(h)]/(R T) g dh
i.e The total pressure (the sum of the two partial pressures) is determined by the weight of the column of atmosphere above it.
(g=9.81, R=8.314)
Taking the following two functions for pO2 and pN2 satisfy the equation above
pO2(h) = pO2(0) exp[- g MO2/(R T) h]
pN2(h) = pN2(0) exp[- g MN2/(R T) h]
(They're analog to the case of a single-component gas)
However, I'm not sure whether it's the whole solution. (If there are other (combinations of) functions for pO2 and pN2 that satisfy the above equation, then any linear combination of the two solutions is also a solution)
So I was hoping someone could either reassure me that this is the only solution, or give me a clue as to what other solutions there are.
|
|
 IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Barometric equation for a mixture of two gasse
« Reply #1 on: Sep 24th, 2007, 3:13pm » |
Quote Modify
|
I seem to remember that in a mixture of ideal gas each gas behaves as if it were alone. The pressures just add.
|
| « Last Edit: Sep 24th, 2007, 3:15pm by Grimbal » |
IP Logged |
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: Barometric equation for a mixture of two gasse
« Reply #2 on: Sep 24th, 2007, 7:05pm » |
Quote Modify
|
First of all, I would write it as a differential equation instead of an integral out to infinity. An easy way to get this equation is to draw a free body diagram for an element of volume with height dh, but it gives the same thing as taking derivative of your integral expression. With the integral to infinity you are making assumptions as to what happens to pressure as you go to infinity.
That is one differential equation, but you have two variables. If you add another equation, such as PN2=constant, or PN2=A*exp(-B*h^2), you can come up with different expressions for PO2. So I think you need add another constraint-- maybe you are supposed to assume the mixture ratio remains 80:20 for all heights.
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Barometric equation for a mixture of two gasse
« Reply #3 on: Sep 25th, 2007, 12:58am » |
Quote Modify
|
on Sep 24th, 2007, 7:05pm, SWF wrote:| First of all, I would write it as a differential equation instead of an integral out to infinity. |
|
Yes, that's how I got the function that I did (well in the single-component case; but then it's easy to see that the addition of two separate such components must fit as well)
Quote:| An easy way to get this equation is to draw a free body diagram for an element of volume with height dh, but it gives the same thing as taking derivative of your integral expression. With the integral to infinity you are making assumptions as to what happens to pressure as you go to infinity. |
|
Well, if you rework it a little, you just get ground pressure minus the pressure of a column from ground level up to h. In any case it's better than the derivation our TA gave, which assumed constant density to derive the differential equation. (It gave the same result, but you should be able to get it without assuming constant density, since density depends on pressure, and pressure is changing with height)
Quote:| That is one differential equation, but you have two variables. If you add another equation, such as PN2=constant, or PN2=A*exp(-B*h^2), you can come up with different expressions for PO2. So I think you need add another constraint-- maybe you are supposed to assume the mixture ratio remains 80:20 for all heights. |
|
Well, we're explicitly asked to give the mole fractions of the gases at 10km, and we're given the 20:80 for ground level. It's bit of a silly question if it's the same.
However, that doesn't change the fact that the equation can be solved with uniform mixture, so we can get any mixture ratio by combining the two sets of solutions.
p*(h) = p(0) exp[- g (.2 MO2 + .8 MN2)/(R T) h]
p*O2(h) = .2 p*(h)
p*N2(h) = .8 p*(h)
So two variables, two solution pairs, does that mean the combinations covers all of them?
|
| « Last Edit: Sep 25th, 2007, 12:59am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: Barometric equation for a mixture of two gasse
« Reply #4 on: Sep 25th, 2007, 6:04pm » |
Quote Modify
|
The the intended solution probably uses Dalton's Law (what Grimbal said) as the additional condition required for a unique solution. Using Dalton's Law would make your equation split into two independent equations: one for PO2 and another for PN2. The sum of them is the solution you had orginally.
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Barometric equation for a mixture of two gasse
« Reply #5 on: Sep 25th, 2007, 11:45pm » |
Quote Modify
|
Hmm, but does Dalton's law really apply here?
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print