 Author
Author |
Topic: U-limit of a sequence (Read 6783 times) |
|
0.999...
Full Member
  

Gender: 
Posts: 156
|
 |
U-limit of a sequence
« on: Apr 29th, 2012, 10:02am » |
 Quote Quote  Modify Modify
|
I am currently reading Set Theory by Thomas Jech (3rd Millennium ed.), and did not like my solution to exercise 7.6:
Let U be an ultrafilter on 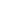 and let <an> be a bounded sequence of countably infinitely many real numbers. Prove that there exists a unique U-limit a such that for every and let <an> be a bounded sequence of countably infinitely many real numbers. Prove that there exists a unique U-limit a such that for every  >0, the set {n: |an-a| < >0, the set {n: |an-a| <  } }  U. U.
Here's my proof. If anyone could either lead me toward something more elegant (e.g. a way to link both cases, perhaps a different line of reasoning in Case I would do that) or confirm that this is the best I can do, I would be grateful.
| hidden: | Case I: U contains only infinite sets (i.e. U is nonprincipal). Since the given sequence is bounded, it has one or more cluster points. Define a mapping from pairs (c,  ) to subsets of ) to subsets of 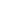 : A(c, : A(c,  ) = {n: |an-c| < ) = {n: |an-c| <  }, where c is a cluster point and }, where c is a cluster point and  > 0. For the sake of contradiction, suppose there is > 0. For the sake of contradiction, suppose there is  > 0 such that A(c, > 0 such that A(c,  ) ) 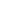 U for all cluster points c. Since A(c, U for all cluster points c. Since A(c, 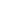 ) ) 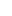 A(c, A(c,  ) when ) when 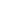 < <  , there exists r such that the property holds for all , there exists r such that the property holds for all  < r and for no < r and for no  > r. Furthermore, A(c,r) > r. Furthermore, A(c,r) 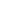 U; otherwise, U would be a principal ultrafilter. Choose U; otherwise, U would be a principal ultrafilter. Choose  > r such that > r such that  < 3r. The set {n: r <= |an-c| < < 3r. The set {n: r <= |an-c| <  } is in U, and so is infinite, which implies that there is a cluster point c' and 0< } is in U, and so is infinite, which implies that there is a cluster point c' and 0< 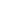 <= ( <= ( -r)/2 < r such that A(c', -r)/2 < r such that A(c', 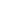 ) )  U. This is a contradiction. U. This is a contradiction.
As  > 0 gets smaller, the cluster points c such that A(c, > 0 gets smaller, the cluster points c such that A(c,  ) )  U are required to be closer to to each other (|c-c'|/2 <= U are required to be closer to to each other (|c-c'|/2 <=  ). Thus, there is a unique cluster point which satisfies the U-limit criterion. Of course, no other point x does, since for some ). Thus, there is a unique cluster point which satisfies the U-limit criterion. Of course, no other point x does, since for some  the set {n: |an-x|< the set {n: |an-x|<  } is finite. } is finite.
Case II: U contains a singleton set {m}. It is clear that {n: |an-an| <  } } 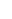 {m}, and thus is in U. {m}, and thus is in U. |
|
| « Last Edit: May 1st, 2012, 6:17am by 0.999... » |
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register