 Author
Author |
Topic: Interesting Limit (Read 7638 times) |
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Interesting Limit
« on: Sep 2nd, 2011, 1:06am » |
 Quote Quote  Modify Modify
|
Find the limit of the following sum when n ->  : :
n 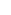 k = 1...n (n2 + k2)-1 k = 1...n (n2 + k2)-1
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: Interesting Limit
« Reply #1 on: Sep 2nd, 2011, 4:20am » |
 Quote Quote  Modify Modify
|
Isn't that just the Riemann sum for the integral of (1+x2)-1 over 0..1? That would make the limit equal to pi divided by four.
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: Interesting Limit
« Reply #2 on: Sep 2nd, 2011, 5:07am » |
 Quote Quote  Modify Modify
|
Here is as formal as a proof as I could get in the short time I worked on this:
| hidden: |
I computed the sum for n=1000. I got 0.7866. pi/4 = 0.7854.
Between an extraordinary coincidence and a very plausible pex being correct, the second option is much more probable.
|
QED.
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Interesting Limit
« Reply #3 on: Sep 2nd, 2011, 11:40am » |
 Quote Quote  Modify Modify
|
pex, you are right, and you probably know a much more elegant proof than that of Grimbal's

|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: Interesting Limit
« Reply #4 on: Sep 3rd, 2011, 2:01am » |
 Quote Quote  Modify Modify
|
 For the sake of completeness: For the sake of completeness:
| hidden: | | Multiply and divide by n2 to get limn to inf (1/n) sumk=1..n (1 + (k/n)2)-1, which is by definition int01 (1 + x2)-1 dx = arctan(1) - arctan(0) = pi/4. |
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register