 Author
Author |
Topic: MATHEMATICS (Read 8220 times) |
|
DOUBELL
Newbie


Posts: 3
|
CAN SOMEONE PROVE BY Mathematical induction that (2r)^3 = 2 (n^2) (n+1)^2 . need help with this one.
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: MATHEMATICS
« Reply #1 on: Sep 1st, 2011, 8:52am » |
 Quote Quote  Modify Modify
|
I think you may have stated the problem incorrectly or incompletely. Since there seem to be no constraints on the values of r and n the two sides are plainly not equal for all values of n and r.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
DOUBELL
Newbie


Posts: 3
|
 |
Re: MATHEMATICS
« Reply #2 on: Sep 1st, 2011, 9:11am » |
 Quote Quote  Modify Modify
|
it is fact correct since for r=1 the LHs is (2)^3 = 8
AND FOR N =1 THE RIGHT HAND SIDE IS 2(1^2) (1+1)^2= 2 (2)^2 = 8.
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: MATHEMATICS
« Reply #3 on: Sep 1st, 2011, 11:41am » |
 Quote Quote  Modify Modify
|
I cannot find any other integer solutions than
r=0, n=-1
r=0, n=0
r=1, n=-2
r=1, n=1.
I don't see what mathematical induction could have to do with it, except perhaps in proving that there are no other solutions (or that there are, but I missed them).
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: MATHEMATICS
« Reply #4 on: Sep 1st, 2011, 12:22pm » |
 Quote Quote  Modify Modify
|
Maybe LHS should be 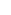 (2n3) (2n3)
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: MATHEMATICS
« Reply #5 on: Sep 1st, 2011, 12:31pm » |
 Quote Quote  Modify Modify
|
on Sep 1st, 2011, 12:22pm, ThudnBlunder wrote:Maybe LHS should be 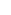 (2n3) (2n3) |
|
I am impressed by your mind-reading skills!
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: MATHEMATICS
« Reply #6 on: Sep 1st, 2011, 12:42pm » |
 Quote Quote  Modify Modify
|
on Sep 1st, 2011, 12:31pm, pex wrote:
I am impressed by your mind-reading skills! |
|
Thank you, pex. [fingernail_polishing_smiley]
|
| « Last Edit: Sep 1st, 2011, 4:01pm by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: MATHEMATICS
« Reply #7 on: Sep 1st, 2011, 12:52pm » |
 Quote Quote  Modify Modify
|
Ah, then it makes sense
base case,
 0..0 (2r)3 = 0 = 2 * 02 * (0+1)2 0..0 (2r)3 = 0 = 2 * 02 * (0+1)2
induction under assumption it's true for every natural number smaller than n:
 0..n (2r)3 0..n (2r)3
= {move last term from sum}
 0..n-1 (2r)3 + (2n)3 0..n-1 (2r)3 + (2n)3
= {invoke induction hypothesis}
2 * n2 * (n-1)2 + 8n * n2
= {regroup terms}
2 * ((n-1)2 + 4n) * n2
= {simplify}
2 * n2 * (n+1)2
|
| « Last Edit: Sep 1st, 2011, 12:54pm by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
DOUBELL
Newbie


Posts: 3
|
 |
Re: MATHEMATICS
« Reply #8 on: Sep 1st, 2011, 1:52pm » |
 Quote Quote  Modify Modify
|
on Sep 1st, 2011, 12:22pm, ThudnBlunder wrote:Maybe LHS should be 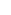 (2n3) (2n3) |
|
THAT IS IN FACT CORRECT ABOUT THE LEFT HAND SIDE
|
|
 IP Logged IP Logged |
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: MATHEMATICS
« Reply #9 on: Feb 29th, 2012, 9:53pm » |
 Quote Quote  Modify Modify
|
Gee. One might ask if induction is valid within an
induction argument itself. What you do think?
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Jack Hadin
Newbie


Gender: 
Posts: 2
|
 |
Re: MATHEMATICS
« Reply #10 on: Oct 29th, 2012, 11:13am » |
 Quote Quote  Modify Modify
|
I think you have recorded the problem wrongly or perhaps incompletely. Because on a search engine appear to be no constraints throughout the principles of r along with n the two sides tend to be plainly not equal for every one of the principles of n also as r.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register