 Author
Author |
Topic: Integral with reciprocal of log x. (Read 4898 times) |
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Integral with reciprocal of log x.
« on: Jul 26th, 2009, 4:37pm » |
 Quote Quote  Modify Modify
|
True or False?
for p >= 0
Integral01 (xp-1)dx/log(x) = log(p+1)
|
| « Last Edit: Jul 26th, 2009, 4:37pm by Aryabhatta » |
 IP Logged IP Logged |
|
|
|
Ronno
Junior Member
 

Gender: 
Posts: 140
|
 |
Re: Integral with reciprocal of log x.
« Reply #1 on: Jul 26th, 2009, 11:54pm » |
 Quote Quote  Modify Modify
|
True.
Proof by Mathematica 
|
| « Last Edit: Jul 26th, 2009, 11:55pm by Ronno » |
 IP Logged IP Logged |
Sarchasm: The gulf between the author of sarcastic wit and the person who doesn't get it..
|
|
|
Obob
Senior Riddler
   

Gender: 
Posts: 489
|
 |
Re: Integral with reciprocal of log x.
« Reply #2 on: Jul 27th, 2009, 8:22am » |
 Quote Quote  Modify Modify
|
Observe that the result is clearly true for p = 0. Differentiate both sides with respect to p, waving your hands a bit (or quoting some theorem) to push the derivative into the integral. d((xp-1)/log(x))/dp = xp, and Integral01 xp dx = 1/(p+1), which is the same answer we get by differentiating the RHS. This implies the LHS = RHS.
Oh, and the restriction p >= 0 is unnecessary; p > -1 will do.
Incidentally, on this page http://en.wikipedia.org/wiki/Differentiation_under_the_integral_sign it is suggested to evaluate Integral01 (x-1) dx/log(x) by considering the problem given here and differentiating under the integral.
|
| « Last Edit: Jul 27th, 2009, 10:20am by Obob » |
 IP Logged IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Re: Integral with reciprocal of log x.
« Reply #3 on: Jul 27th, 2009, 10:37am » |
 Quote Quote  Modify Modify
|
Correct!
Not sure about the p > -1. The theorem statement I had at hand (in Apostol's analysis book) seemed to require df(x,p)/dp to be bounded for the differentiation under the integral sign to work.
Do you know of any other version of the theorem which lets p > -1?
The wiki page having this is just a coincidence!
|
|
 IP Logged IP Logged |
|
|
|
Obob
Senior Riddler
   

Gender: 
Posts: 489
|
 |
Re: Integral with reciprocal of log x.
« Reply #4 on: Jul 27th, 2009, 11:49am » |
 Quote Quote  Modify Modify
|
The result might not be quite as straightforward, but it should certainly be true.
One way to set it up would be to look instead at G(p,  ) = ) =    (xp-1) dx/log(x). We have G(0, (xp-1) dx/log(x). We have G(0,  ) = 0, and interchanging interal and derivative is valid for ) = 0, and interchanging interal and derivative is valid for  > 0, so > 0, so
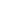 G/ G/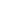 p = p =    xp= (1 - xp= (1 -  1+p)/(1+p). 1+p)/(1+p).
Thus
G(p,  ) = - ) = -  p p (1 - (1 -  1+p) dp/(1+p) = log(p+1) + 1+p) dp/(1+p) = log(p+1) +     1+p dp/(1+p) 1+p dp/(1+p)
for  > 0. Now since for fixed p > -1 the integrand is absolutely convergent, for fixed p we see that G(p, > 0. Now since for fixed p > -1 the integrand is absolutely convergent, for fixed p we see that G(p, ) is a continuous function of ) is a continuous function of  at at  = 0. Therefore = 0. Therefore
G(p, 0) = log(p+1) + lim  0 0     1+p dp/(1+p). 1+p dp/(1+p).
But the limit on the RHS is clearly zero for p > -1 by the dominated convergence theorem since the integrand is dominated by a bounded function and approaches 0 pointwise almost everywhere as   0. 0.
Another big hammer approach which should be valid: allow p to be complex. If the real part of p is bigger than -1, then F(p) =    (xp-1) dx/log(x) is defined. Moreover, I think it should be possible to show F is a complex analytic function. But it agrees with log(p+1) for Re p (xp-1) dx/log(x) is defined. Moreover, I think it should be possible to show F is a complex analytic function. But it agrees with log(p+1) for Re p  0, which implies it must equal log(p+1) everywhere it is defined. 0, which implies it must equal log(p+1) everywhere it is defined.
Generally speaking, I think absolute convergence is the main thing you have to be worried about when applying this kind of argument. There is another argument here http://mathworld.wolfram.com/IntegrationUndertheIntegralSign.html which derives the same formula by applying Fubini's theorem (interchanging two integrals). The only thing you really have to worry about for Fubini's theorem is absolute convergence.
|
| « Last Edit: Jul 27th, 2009, 12:07pm by Obob » |
 IP Logged IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Re: Integral with reciprocal of log x.
« Reply #5 on: Jul 27th, 2009, 12:19pm » |
 Quote Quote  Modify Modify
|
Right, I was expecting some arguments like that to work... but was looking at directly applying a stronger theorem, seems like Fubini's is one which will work.
Thanks!
|
| « Last Edit: Jul 27th, 2009, 12:19pm by Aryabhatta » |
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register