wu :: forums « wu :: forums - Cubic Diophantine Equation » Welcome, Guest. Please Login or Register. Feb 17th, 2025, 2:55pm

RIDDLES SITE WRITE MATH! Home Help Search Members Login Register

wu :: forums    riddles    putnam exam (pure math) (Moderators: Eigenray, william wu, SMQ, Icarus, towr, Grimbal)    Cubic Diophantine Equation « Previous topic | Next topic » Pages: 1  Reply Notify of replies Send Topic Print    Author  Topic: Cubic Diophantine Equation  (Read 1502 times) Barukh Uberpuzzler     Gender: Posts: 2276 Cubic Diophantine Equation   « on: Oct 31st, 2008, 10:15am » Quote Modify Let p = 2n + 1 be a prime number.  How many integer solutions mod p has the following equation:   y2 - x3 + 3x - 1 = 0 mod p   Note: The equation was changed. « Last Edit: Oct 31st, 2008, 9:47pm by Barukh » IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: Cubic Diophantine Equation   « Reply #1 on: Oct 31st, 2008, 3:36pm » Quote Modify Well, to start with, it is the integer closest to p which is congruent to the coefficient of xp-1 in -(x3-3x+1)(p-1)/2. « Last Edit: Oct 31st, 2008, 10:19pm by Eigenray » IP Logged Barukh Uberpuzzler     Gender: Posts: 2276 Re: Cubic Diophantine Equation   « Reply #2 on: Oct 31st, 2008, 9:45pm » Quote Modify Sorry, I mis-stated the problem (which made it much harder IMHO).   Let's try to go with the easier one first...   Sorry for inconvenience. IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: Cubic Diophantine Equation   « Reply #3 on: Oct 31st, 2008, 10:25pm » Quote Modify Yes that is much easier.  But why is p a Fermat prime?  It's enough that p is not 1 mod 3.  Or did you have a different proof in mind?   Theorem: For a cubic polynomial f(x), the number of solutions to y2 f(x) mod p is congruent, mod p, to the coefficient of xp-1 in -f(x)(p-1)/2.   But I've seen this result before so it would feel like cheating to give the proof right away.  Does someone else want to try? « Last Edit: Oct 31st, 2008, 10:52pm by Eigenray » IP Logged Barukh Uberpuzzler     Gender: Posts: 2276 Re: Cubic Diophantine Equation   « Reply #4 on: Nov 1st, 2008, 12:26am » Quote Modify on Oct 31st, 2008, 10:25pm, Eigenray wrote: It's enough that p is not 1 mod 3.  Or did you have a different proof in mind? No, your condition is sufficient, and the proof I had in mind uses this condition. My formulation is a special case of that.   Quote: Theorem: For a cubic polynomial f(x), the number of solutions to y2 f(x) mod p is congruent, mod p, to the coefficient of xp-1 in -f(x)(p-1)/2. I haven't heard about this theorem before, but after seeing it, it does make sense, and probably is based on Euler criterion for quadratic residues.   IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: Cubic Diophantine Equation   « Reply #5 on: Nov 1st, 2008, 6:31pm » Quote Modify It suddenly hit me that there's a simpler solution that I didn't notice because I had been thinking about the harder problem: everything is a cube. « Last Edit: Nov 1st, 2008, 6:32pm by Eigenray » IP Logged Barukh Uberpuzzler     Gender: Posts: 2276 Re: Cubic Diophantine Equation   « Reply #6 on: Nov 2nd, 2008, 8:31am » Quote Modify on Nov 1st, 2008, 6:31pm, Eigenray wrote: everything is a cube. If I get you right, yes, that's the solution I had in mind. Very nice! IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: Cubic Diophantine Equation   « Reply #7 on: Nov 2nd, 2008, 11:50am » Quote Modify Here are two related problems: how many solutions are there to:   (1) y2 = x3 + ax mod p, p a Mersenne prime   (2) y2 = x3 + ax2 mod p.     Both can be answered using the theorem I quoted, but there are also more direct(?) proofs. « Last Edit: Nov 2nd, 2008, 11:51am by Eigenray » IP Logged Barukh Uberpuzzler     Gender: Posts: 2276 Re: Cubic Diophantine Equation   « Reply #8 on: Nov 3rd, 2008, 11:38pm » Quote Modify on Nov 2nd, 2008, 11:50am, Eigenray wrote: Here are two related problems: how many solutions are there to:   (1) y2 = x3 + ax mod p, p a Mersenne prime   (2) y2 = x3 + ax2 mod p. Assuming a 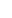0 mod p, I get the following:   1)  p 2)  p - (a/p), where the last is Legendre symbol. IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: Cubic Diophantine Equation   « Reply #9 on: Nov 4th, 2008, 11:11pm » Quote Modify Yep.  I thought it was interesting how the three problems can be solved individually using quite distinct arguments, or all using that one theorem I quoted. IP Logged Pages: 1  Reply Notify of replies Send Topic Print Forum Jump: ----------------------------- riddles -----------------------------  - easy   - medium   - hard   - what am i   - what happened   - microsoft   - cs => putnam exam (pure math)   - suggestions, help, and FAQ   - general problem-solving / chatting / whatever ----------------------------- general -----------------------------  - guestbook   - truth   - complex analysis   - wanted   - psychology   - chinese « Previous topic | Next topic »

Powered by YaBB 1 Gold - SP 1.4!
Forum software copyright © 2000-2004 Yet another Bulletin Board