 Author
Author |
Topic: Integral Solutions (Read 1413 times) |
|
l4z3r
Newbie


Posts: 10
|
 |
Integral Solutions
« on: Aug 29th, 2008, 4:46am » |
 Quote Quote  Modify Modify
|
a function is defined as:
f: Z(+) --> Z
f(m,n) = (n3 + 1)/ (mn - 1)
where Z(+) denotes the set of positive integers and Z the set of integers.
Find all the solutions for (m,n)
EDIT: f(m,n) not f(x)
|
| « Last Edit: Aug 29th, 2008, 5:42am by l4z3r » |
 IP Logged IP Logged |
|
|
|
l4z3r
Newbie


Posts: 10
|
 |
Re: Integral Solutions
« Reply #2 on: Aug 29th, 2008, 5:42am » |
 Quote Quote  Modify Modify
|
ah. meant f(m,n). sorry.
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Integral Solutions
« Reply #3 on: Aug 29th, 2008, 5:58am » |
 Quote Quote  Modify Modify
|
So, in other words, "find all  , , 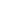    such that ( such that (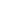  + 1) / ( + 1) / ( 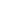 - 1) - 1)   ", right? ", right?
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
l4z3r
Newbie


Posts: 10
|
 |
Re: Integral Solutions
« Reply #4 on: Aug 29th, 2008, 7:00am » |
 Quote Quote  Modify Modify
|
yes. hint:use n3+1  1(mod3) and mn-1 1(mod3) and mn-1  -1 (mod n) (number theory) -1 (mod n) (number theory)
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Integral Solutions
« Reply #5 on: Aug 29th, 2008, 11:53am » |
 Quote Quote  Modify Modify
|
If (m,n) is a solution, then (m, (m2+n)/(mn-1)) is also; then use the ideas that appear here (and which should appear here).
Or, you can proceed more directly by writing n3+1 = (mn-1)((an-m)n-1) and bounding.
|
|
 IP Logged IP Logged |
|
|
|
l4z3r
Newbie


Posts: 10
|
 |
Re: Integral Solutions
« Reply #6 on: Aug 30th, 2008, 5:34am » |
 Quote Quote  Modify Modify
|
hmm. good one. I agree with the first part.
If (m,n) is a solution, then (m, (m2+n)/(mn-1)) is also
but, instead of (mn-1)((an-m)n-1) i feel a better alternative would be (kn-1)(mn-1). Gives the answer in lesser steps, i think.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register