 Author
Author |
Topic: Limit of Integral (Read 765 times) |
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Limit of Integral
« on: Jul 12th, 2008, 9:11am » |
 Quote Quote  Modify Modify
|
What is 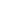 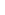 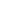  (1 + t/k)ke-t.dt/ (1 + t/k)ke-t.dt/ k from t = 0 to k from t = 0 to 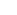 ? ?
k->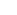
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Limit of Integral
« Reply #1 on: Jul 12th, 2008, 11:28am » |
 Quote Quote  Modify Modify
|
I think it helps to know that the median of Poisson-k is around k.
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Limit of Integral
« Reply #2 on: Aug 7th, 2008, 10:04am » |
 Quote Quote  Modify Modify
|
| hidden: | By induction we have  0 0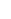 tre-tdt = r!. So the integral is tre-tdt = r!. So the integral is
 r=0k C(k,r)(k-r)!/kk-r = k! ek/kk r=0k C(k,r)(k-r)!/kk-r = k! ek/kk  r=0k e-kkr/r! r=0k e-kkr/r!
= k! ek/kk Pr( Pk  k ), k ),
where Pk is Poisson-k. Pk has the same distribution as the sum of k P1's, so by the central limit theorem, (Pk-k)/ {k} converges to standard normal, and Pr( Pk {k} converges to standard normal, and Pr( Pk  k ) converges to 1/2. By Stirling, k! ek/kk ~ k ) converges to 1/2. By Stirling, k! ek/kk ~  {2 {2 k}, and it follows that the limit is k}, and it follows that the limit is  { { /2}. /2}. |
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register