 Author
Author |
Topic: SIGMAarctan(2/n^2) (Read 1669 times) |
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
SIGMAarctan(2/n^2)
« on: May 20th, 2008, 5:37am » |
 Quote Quote  Modify Modify
|

Evaluate  tan-1(2/n2) tan-1(2/n2)
n=1
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: SIGMAarctan(2/n^2)
« Reply #1 on: May 20th, 2008, 10:44am » |
 Quote Quote  Modify Modify
|
135o
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: SIGMAarctan(2/n^2)
« Reply #2 on: May 20th, 2008, 10:52am » |
 Quote Quote  Modify Modify
|
on May 20th, 2008, 10:44am, Barukh wrote:
Was that computer-assisted? 
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: SIGMAarctan(2/n^2)
« Reply #3 on: May 20th, 2008, 11:19am » |
 Quote Quote  Modify Modify
|
on May 20th, 2008, 10:52am, ThudanBlunder wrote:
Was that computer-assisted? 
|
|
No.
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: SIGMAarctan(2/n^2)
« Reply #4 on: May 20th, 2008, 11:27am » |
 Quote Quote  Modify Modify
|
on May 20th, 2008, 11:19am, Barukh wrote:
Then I'm beginning to believe our literary tastes are similar. 
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: SIGMAarctan(2/n^2)
« Reply #5 on: May 20th, 2008, 11:14pm » |
 Quote Quote  Modify Modify
|
| hidden: | Solution is based on the following identity:
tan-1(2/n2) = tan-1(n+1) - tan-1(n-1) |
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: SIGMAarctan(2/n^2)
« Reply #6 on: May 21st, 2008, 2:45am » |
 Quote Quote  Modify Modify
|
Or less cleverly, working out the first few partial sums suggests
| hidden: | | arctan{-(n-1)(n+2)/[n(n-3)]} + arctan{2/n2} = arctan{-n(n+3)/[(n+1)(n-2)]} |
|
|
 IP Logged IP Logged |
|
|
|
william wu
wu::riddles Administrator
    


Gender: 
Posts: 1291
|
 |
Re: SIGMAarctan(2/n^2)
« Reply #7 on: May 21st, 2008, 3:59am » |
 Quote Quote  Modify Modify
|
Digression: As a knee jerk reaction, I took the derivative of the summand, and tried summing that instead. Not that that would lead to anything relevant for this problem ... but I ended up with something that surprised me:
d/dx [ArcTan[2/x^2]] = -(4 x)/(4 + x^4)
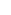 -(4 n)/(4 + n^4) = -3/2 -(4 n)/(4 + n^4) = -3/2
OK, now someone explain why I shouldn't be surprised 
|
| « Last Edit: May 21st, 2008, 4:00am by william wu » |
 IP Logged IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register