Author |
Topic: Summation of series (Read 2767 times) |
|
Optimus Prime
Newbie
Gender: 
Posts: 2
|
 |
Summation of series
« on: Jan 21st, 2008, 8:19pm » |
 Quote  Modify
|
Find the sum of the first n terms of the following series:
1/7 + 1/77 + 1/777 + ... up to n-th term
|
|
 IP Logged |
|
|
|
ThudnBlunder
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Summation of series
« Reply #1 on: Jan 21st, 2008, 10:23pm » |
Quote Modify
|
So we need to find
n
(9/7) 1/(10k - 1)
k=1
|
| « Last Edit: Jan 22nd, 2008, 7:56am by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Summation of series
« Reply #2 on: Jan 24th, 2008, 5:13pm » |
Quote Modify
|
If Optimus Prime has a nice answer for this, it would be interesting from a number theory point-of-view.
If we let x = 0.1, we can rewrite T&B's summation as
k=1..n xk/(1 - xk) = k=1..n j=1.. xkj = m=1.. d(m; n) xm,
where d(m; n) = |{ d  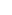 : d | m and d <= n}| is the number of divisors of m less than or equal to n.
Thus a generalized solution to this problem could provided a means of generating the values of d(m; n).
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print