 Author
Author |
Topic: Prove/Disprove a function is continuous (Read 1485 times) |
|
archau
Newbie


Posts: 5
|
 |
Prove/Disprove a function is continuous
« on: Dec 13th, 2007, 4:59pm » |
 Quote Quote  Modify Modify
|
Consider the euclidean space of all (2n+1) x (2n+1) matrices.
Prove/Disprove that the function mapping an element A to is largest real eigenvalue is continuous.
Note: There was a mistake in the original statement of the problem so I changed it.
|
| « Last Edit: Dec 15th, 2007, 6:54am by archau » |
 IP Logged IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Re: Prove a function is continuous
« Reply #1 on: Dec 14th, 2007, 2:16am » |
 Quote Quote  Modify Modify
|
Perhaps this should be in the putnam section.
|
|
 IP Logged IP Logged |
|
|
|
Obob
Senior Riddler
   

Gender: 
Posts: 489
|
 |
Re: Prove a function is continuous
« Reply #2 on: Dec 14th, 2007, 8:11pm » |
 Quote Quote  Modify Modify
|
I think this result is false. Consider the family of polynomials (x + 1)(x2 + a2), where a is a nonzero real number. Expanding, this is the polynomial x3 + x2 + a2x + a2. This is the characteristic polynomial of the companion matrix
0 0 -a2
1 0 -a2
0 1 -1
So the eigenvalues of this matrix are -1, ia, and -ia. Hence the largest real eigenvalue is -1. But as we let a->0, the eigenvalues of the limit matrix are -1, 0, and 0, so that the largest real eigenvalue is 0.
The problem here is that a conjugate pair of complex eigenvalues can specialize in the limit to a real eigenvalue with multiplicity two.
Here's a problem for somebody else to solve: Show that the problem becomes true again if we consider instead the space of symmetric n x n matrices.
|
| « Last Edit: Dec 14th, 2007, 8:14pm by Obob » |
 IP Logged IP Logged |
|
|
|
archau
Newbie


Posts: 5
|
 |
Re: Prove a function is continuous
« Reply #3 on: Dec 15th, 2007, 6:52am » |
 Quote Quote  Modify Modify
|
You are correct, I will add a correction to the original problem.
|
|
 IP Logged IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Re: Prove a function is continuous
« Reply #4 on: Dec 15th, 2007, 12:58pm » |
 Quote Quote  Modify Modify
|
on Dec 14th, 2007, 8:11pm, Obob wrote:
Here's a problem for somebody else to solve: Show that the problem becomes true again if we consider instead the space of symmetric n x n matrices. |
|
Do you mean symmetric real matrices (sorry if it is obvious, I am rusty...)
In which case, I think the Rayleigh Quotient should somehow do it, though I am not confident...
|
| « Last Edit: Dec 15th, 2007, 1:04pm by Aryabhatta » |
 IP Logged IP Logged |
|
|
|
Obob
Senior Riddler
   

Gender: 
Posts: 489
|
 |
Re: Prove/Disprove a function is continuous
« Reply #5 on: Dec 15th, 2007, 1:22pm » |
 Quote Quote  Modify Modify
|
Yes, I did mean real symmetric; otherwise in more generality you could do it for complex Hermitian matrices.
That idea does seem to be fruitful, Aryhabhatta. It's actually quite a bit nicer than what I was thinking of. Anybody care to flesh out the details?
|
|
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: Prove/Disprove a function is continuous
« Reply #6 on: Dec 28th, 2007, 2:09am » |
 Quote Quote  Modify Modify
|
I thing the main problem here is the unstability of being real.
To select one from the complex numbers is not trivial.
What about the mapping to set of eigenvalues with multicities. Is this mapping (from arbitrary matrices) continuous?
|
| « Last Edit: Dec 28th, 2007, 2:09am by Hippo » |
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Prove/Disprove a function is continuous
« Reply #7 on: Jan 6th, 2008, 6:22pm » |
 Quote Quote  Modify Modify
|
on Dec 28th, 2007, 2:09am, Hippo wrote:I thing the main problem here is the unstability of being real.
To select one from the complex numbers is not trivial.
What about the mapping to set of eigenvalues with multicities. Is this mapping (from arbitrary matrices) continuous? |
|
Yes, exactly. Choosing the largest real eigenvalue is a composition of two functions: (matrix) -> (set of eigenvalues) -> (largest real eigenvalue), but only the first is continuous.
To state this formally: fix a matrix A, with (multi-)set of eigenvalues S. Then for any  >0, there exists a >0, there exists a 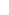 >0 such that: whenever each entry of A' is within >0 such that: whenever each entry of A' is within 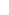 of the corresponding entry of A, there exists a bijection between S and S' such that corresponding elements are within of the corresponding entry of A, there exists a bijection between S and S' such that corresponding elements are within  of each other. of each other.
For otherwise, there's an  >0 for which we can pick a sequence of matrices An >0 for which we can pick a sequence of matrices An  A entry-wise, but where no Sn is uniformly within A entry-wise, but where no Sn is uniformly within  of S under any ordering. of S under any ordering.
Now put an arbitrary ordering on S and Sn so that they become elements of 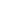 N. Now, two sets close in one order need not be in another, but this is okay: there are finitely many coordinates, and moreover, since An N. Now, two sets close in one order need not be in another, but this is okay: there are finitely many coordinates, and moreover, since An  A, the entries of {An} are all bounded, and therefore so are the entries of {Sn}. So by compactness, we may pass to a subsequence such that Sn A, the entries of {An} are all bounded, and therefore so are the entries of {Sn}. So by compactness, we may pass to a subsequence such that Sn  S' S'  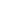 N. N.
Let pn(x) =  (x-Sn(i)) be the characteristic polynomial of An. For any x, pn(x) (x-Sn(i)) be the characteristic polynomial of An. For any x, pn(x)  p'(x) = p'(x) =  (x-S'(i)). But also pn(x) (x-S'(i)). But also pn(x)  p(x) = p(x) =  (x-S(i)). Therefore S=S', and this contradicts our assumption that each Sn is at least (x-S(i)). Therefore S=S', and this contradicts our assumption that each Sn is at least  away from S in some coordinate. away from S in some coordinate.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register