 Author
Author |
Topic: Common Eigenvector Condition (Read 5398 times) |
|
william wu
wu::riddles Administrator
    


Gender: 
Posts: 1291
|
 |
Common Eigenvector Condition
« on: Dec 12th, 2007, 4:08pm » |
 Quote Quote  Modify Modify
|
Let A and B be square matrices. Prove the following:
if Rank(A·B – B·A) <= 1,
then A and B have at least one eigenvector in common.
Source: W. Kahan
|
| « Last Edit: Dec 12th, 2007, 4:08pm by william wu » |
 IP Logged IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Common Eigenvector Condition
« Reply #1 on: Dec 15th, 2007, 7:06pm » |
 Quote Quote  Modify Modify
|
Please pardon this aside, Wu (little progress so far on this interesting problem). A novel I am reading says that "wu" is "five" in Mandarin, and that the chinese character represents the five elements of herbal medecine, metal, wood, water, fire, and earth. Is this true?
|
|
 IP Logged IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Re: Common Eigenvector Condition
« Reply #2 on: Dec 17th, 2007, 5:49pm » |
 Quote Quote  Modify Modify
|
Here is a partial try at the problem: special case when AB = BA.
Say l is an eigenvalue of A and x is a correponding eigenvector.
Then we have that
A(Bx) = B(Ax) = l(Bx)
Thus Bx is also an eigenvector of A.
Consider the eigenspace E(l,A) corresponding to A and l.
We can show that E(l,A) is invariant under B.
I think we can show that a finite dimensional space which is invariant under a linear transform must contain an eigenvector of that transform.
Since E(l,A) is invariant under B, it must contain an eigenvector of B... hence A and B have a common eigenvector.
|
|
 IP Logged IP Logged |
|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Common Eigenvector Condition
« Reply #3 on: Dec 17th, 2007, 7:17pm » |
 Quote Quote  Modify Modify
|
The case AB=BA is in a textbook, Aryabhatta, along with your proof (can't recall a reference). As for the part of your proof that you left out, let W be a subspace invariant under a linear transformation T and let w=/=0 be in W. Consider the polynomial p(x) of least degree such that p(T)w=0. (I used your trick for my posted problem concerning two rational matrices that commute. Didn't know then that there was a more elementary solution)
|
|
 IP Logged IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Re: Common Eigenvector Condition
« Reply #4 on: Dec 17th, 2007, 7:56pm » |
 Quote Quote  Modify Modify
|
on Dec 17th, 2007, 7:17pm, ecoist wrote:| I used your trick for my posted problem concerning two rational matrices that commute. |
|
Which problem is that? I must have missed it. Can you please post a link?
|
|
 IP Logged IP Logged |
|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Common Eigenvector Condition
« Reply #5 on: Dec 17th, 2007, 8:26pm » |
 Quote Quote  Modify Modify
|
My damn updated IE won't let me copy urls! The problem is on page 6 of putnam exam entitled "Can these rational matrices commute?"
|
|
 IP Logged IP Logged |
|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Common Eigenvector Condition
« Reply #6 on: Dec 30th, 2007, 9:18pm » |
 Quote Quote  Modify Modify
|
It is obvious that, if A and B have a common eigenvector, then that vector must lie in the null space of AB-BA. But, so far, I can't even prove that A has any eigenvector in the null space of AB-BA! A could have only one eigenvector (modulo scalar multiiples)! Also, I don't yet see the significance of AB-BA having rank <1. This fact implies that the minimum polynomial of AB-BA is x or x2, but it doesn't seem to help. I even wondered if there are any matrices A and B at all such that AB-BA has rank 1. I stumbled on such a pair.
A=|0 0|, B=|1 1|.
|1 -1|, |1 1|
This A and B have the common eigenvector (1,1).
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Common Eigenvector Condition
« Reply #7 on: Jan 7th, 2008, 9:52pm » |
 Quote Quote  Modify Modify
|
on Dec 30th, 2007, 9:18pm, ecoist wrote:| But, so far, I can't even prove that A has any eigenvector in the null space of AB-BA! |
|
I can at least show this much: suppose C = AB-BA has rank 1. Adding a scalar multiple of I to A doesn't change anything, so we can assume A is invertible.
For any k, CAk has rank  1, and trace 0, so CAkCAk=0, and therefore CAkC=0. So the image of span<AkC> is a non-zero A-invariant subspace of K = ker C. So A has some eigenspace E intersecting K non-trivially. 1, and trace 0, so CAkCAk=0, and therefore CAkC=0. So the image of span<AkC> is a non-zero A-invariant subspace of K = ker C. So A has some eigenspace E intersecting K non-trivially.
Now B(E  K) K) 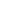 E, so if E E, so if E 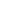 K (for example, if dim E =1), then we're done. But otherwise I don't know what to do. K (for example, if dim E =1), then we're done. But otherwise I don't know what to do.
I don't think we can use the same trick to show CMC=0 for any monomial M in A,B, because tr(CM) may not be 0...
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Common Eigenvector Condition
« Reply #8 on: Mar 20th, 2008, 5:05pm » |
 Quote Quote  Modify Modify
|
We have two obvious A-invariant subspaces, Ker(A) and Im(A). But at least one of them must also be B-invariant:
Suppose Ker(A) is not B-invariant. Pick x with Ax=0, ABx  0. Then Cx = ABx - BAx = ABx 0. Then Cx = ABx - BAx = ABx  0, and since C has rank 1, it follows Im(C) 0, and since C has rank 1, it follows Im(C) 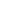 Im(A). But BA = AB - C, so Im(BA) Im(A). But BA = AB - C, so Im(BA) 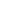 Im(A), i.e., Im(A) is B-invariant. Im(A), i.e., Im(A) is B-invariant.
Now, if A is a scalar multiple of I, it is obvious. Otherwise, we can add a scalar multiple of I to A so that both Ker(A) and Im(A) are non-zero, so at least one of them is invariant under both A and B. Passing to this subspace, we induct until the dimension is 1, where the problem is trivial.
|
|
 IP Logged IP Logged |
|
|
|
william wu
wu::riddles Administrator
    


Gender: 
Posts: 1291
|
 |
Re: Common Eigenvector Condition
« Reply #9 on: May 19th, 2008, 1:08pm » |
 Quote Quote  Modify Modify
|
on Dec 15th, 2007, 7:06pm, ecoist wrote:| Please pardon this aside, Wu (little progress so far on this interesting problem). A novel I am reading says that "wu" is "five" in Mandarin, and that the chinese character represents the five elements of herbal medecine, metal, wood, water, fire, and earth. Is this true? |
|
Digressing, here's a late reply to this:
- Regarding the interpretation of "five" that you mentioned, I've seen that in some references. The original character was an hourglass, and later it morphed into the modern-day character. "The two principles yin and yang, begetting the five elements, between heaven and earth." - Wieger. However, there isn't always agreement on the interpretations; Karlgren calls it "far-fetched". It's difficult to know what the original derivation was.
- Not sure if you were wondering whether my last name means "five", but in case you did, here are some interesting facts about Chinese:
- Chinese is ridden with homonyms. The romanization "wu" has over 100 different characters corresponding to it.
- Furthermore, Chinese is a tonal language. In Mandarin, there are four tones: so to trim down the possibilities, we can write wu1, wu2, wu3, and wu4, all corresponding to different intonations of the same phonetic sound. However, the ratio of 4:114 is still pretty low. So we have to rely on context to make sense of things -- isolated words with no context make no sense.
- Given the odds, its not surprising that my last name's (wu2) is totally different from the (wu3) that means five.
|
|
 IP Logged IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register