Author |
Topic: Ball-bearing on Sphere (Read 3231 times) |
|
ThudnBlunder
Uberpuzzler
The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Ball-bearing on Sphere
« on: Nov 26th, 2007, 12:01pm » |
 Quote  Modify
|
I have seen this one before, hopefully not here:
A slippery ball-bearing is placed in equilibrium on the top of a sphere. It is given a negligibly small impulse which makes it slide down the sphere. Where does it leave the surface of the sphere?
Pre-emptive assumptions for nitpickers:
1) The radius of the ball-bearing is negligible compared with the sphere.
2) The ball-bearing slides without rolling - ie. there is no friction.
What can we say if the ball-bearing rolls without slipping?
|
| « Last Edit: Nov 26th, 2007, 2:25pm by ThudnBlunder » |
 IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Ball-bearing on Sphere
« Reply #1 on: Nov 26th, 2007, 12:28pm » |
Quote Modify
|
Let the ball-bearing have slid through an angle  around a sphere or radius R. From conservation of energy we have mgh = mv2/2  v2 = 2gR(1 - cos ). The ball-bearing will leave the sphere when the centrifugal force due to its velocity along the surface of the sphere is equal to the radial component of the acceleration due to gravity: v2/R = g cos . Substituting for velocity we have 2gR(1 - cos )/R = g cos 2 - 2 cos = cos = cos-1 (2/3) 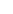 48.2o (declination from vertical), regardless of the radius of the sphere or the acceleration of gravity!
The case where the ball-bearing rolls should be similar, with the addition of a term for energy stored as internal angular momentum of the ball-bearing. In general, we can say that the rolling ball bearing will leave the surface of the sphere later than in the sliding case, as some of the gravitational potential energy (which was converted entirely to kinetic energy in the sliding case) will now be stored in the internal rotational momentum of the bearing, and so the rolling bearing will be traveling slightly slower than an equivalent sliding bearing at any given point.
--SMQ
|
| « Last Edit: Dec 5th, 2007, 5:50am by SMQ » |
IP Logged |
--SMQ
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print