 Author
Author |
Topic: Calculus of variations (Read 1175 times) |
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Calculus of variations
« on: Oct 6th, 2007, 2:25pm » |
 Quote Quote  Modify Modify
|
Find the plane curve of fixed perimeter and maximum area.
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Calculus of variations
« Reply #1 on: Oct 6th, 2007, 2:53pm » |
 Quote Quote  Modify Modify
|
The answer is easy enough, of course. A curve doesn't have an area 
And the curve that encloses the largest area, given the length of the perimeter, is of course a circle.
But I still can't remember how to solve it; I'd have to consult my class notes (and considering how they're written, that might not help much either).
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Calculus of variations
« Reply #2 on: Oct 6th, 2007, 2:59pm » |
 Quote Quote  Modify Modify
|
on Oct 6th, 2007, 2:53pm, towr wrote:The answer is easy enough, of course. A curve doesn't have an area 
And the curve that encloses the largest area, given the length of the perimeter, is of course a circle.
But I still can't remember how to solve it; I'd have to consult my class notes (and considering how they're written, that might not help much either). |
|
Cool, I forgot I had posted that problem from my book earlier. Yea well the answer is easy, proving is the challenge!! 
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Pietro K.C.
Full Member
  

 

Gender: 
Posts: 213
|
 |
Re: Calculus of variations
« Reply #3 on: Oct 17th, 2007, 1:36pm » |
 Quote Quote  Modify Modify
|
Quote:| A curve doesn't have an area |
|
Watch out!  I myself tried to prove this for a couple of days, only to find out that, amazingly, some curves do have an area. Indeed, it is possible for a curve to fill out an entire square! The technical statement is that there is a continuous I myself tried to prove this for a couple of days, only to find out that, amazingly, some curves do have an area. Indeed, it is possible for a curve to fill out an entire square! The technical statement is that there is a continuous
 : [0,1] --> [0,1] x [0,1] : [0,1] --> [0,1] x [0,1]
which is surjective (but it is never injective). Though we may at first be surprised that we cannot map the "thin" space [0,1] into the "fat" space [0,1]2 without repeating values --- which intuitively only "spends" our already very "scarce" domain set --- the fact is that the injectivity restriction is much direr, because the curve then has to dodge itself in ingenious ways to get to places it hasn't been yet.
So ingenious, in fact, that it's impossible.
In the simpler constructions, like the Peano curve,  is very strongly not injective, but, as suggested by Hilbert and proved by Polya, it is possible to do it with non-injectivity degree 3: every point of the square having at most 3 preimages. The book "Space-Filling Curves" by Hans Sagan gives quite a nice tour of the subject. is very strongly not injective, but, as suggested by Hilbert and proved by Polya, it is possible to do it with non-injectivity degree 3: every point of the square having at most 3 preimages. The book "Space-Filling Curves" by Hans Sagan gives quite a nice tour of the subject.
The Wikipedia article
The proof of non-injectivity of a square-filling curve is actually quite simple: if X is a compact topological space and f : X-->Y a bijective continuous function, then f is actually a homeomorphism; and any number of topological properties distinguish [0,1] from [0,1]2 (e.g. it is possible to disconnect [0,1], but not [0,1]2, by removing one point).
A natural question might be: is there a curve which has both a perimeter and positive area?
|
| « Last Edit: Oct 17th, 2007, 1:38pm by Pietro K.C. » |
 IP Logged IP Logged |
"I always wondered about the meaning of life. So I looked it up in the dictionary under 'L' and there it was --- the meaning of life. It was not what I expected." (Dogbert)
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Calculus of variations
« Reply #4 on: Oct 17th, 2007, 3:04pm » |
 Quote Quote  Modify Modify
|
I actually knew about the Hilbert curve; it came up in one of my classes once..
I think it's safe to say any curve of finite length lacks an area, though.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Pietro K.C.
Full Member
  

 

Gender: 
Posts: 213
|
 |
Re: Calculus of variations
« Reply #5 on: Oct 17th, 2007, 5:11pm » |
 Quote Quote  Modify Modify
|
About the original question, I always thought it should be doable by plain symmetry considerations. If S1 is the unit circle and
 : S1 : S1  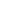 2 2
is continuous and injective, by the Jordan curve theorem it bounds a region R, and  (S1) is its boundary, denoted (S1) is its boundary, denoted 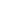 R. If we suppose for a moment that R. If we suppose for a moment that 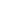 R has zero measure, then R is measurable (has a well-defined area), and the function R has zero measure, then R is measurable (has a well-defined area), and the function
g(a) = area of the part of R that lies to the left of the line x=a
is continuous. Since, for large negative a, g(a) = 0, and for large positive a, g(a) = area of R, there must be some place somewhere in between where the line x=a exactly bisects the area of R. We therefore choose the half with smaller perimeter and mirror it across x=a, obtaining a curve which has at most the same perimeter, same area, and is symmetric about x=a.
Of course, all this works for lines in any direction, not just vertical ones. Enumerate the rational numbers in a sequence as (qn)n 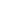 , and define a sequence of regions , and define a sequence of regions
R0 = R
Rn+1 = F(qn,Rn)
where F(qn, ) is the process just indicated, but using a symmetry line that makes an angle qn with the x-axis. ) is the process just indicated, but using a symmetry line that makes an angle qn with the x-axis.
Supposing R to be convex (a reasonable assumption for a maximizing curve, but which I can't prove off the top of my head), each F(qn, ) acts naturally on the curve's parametrization function ) acts naturally on the curve's parametrization function  , turning it into one which describes the boundary of the new region. With some work, I think one can then prove that, with copious abuse of notation, , turning it into one which describes the boundary of the new region. With some work, I think one can then prove that, with copious abuse of notation,
F(qn, ) )  circle as n circle as n  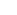 . .
Any thoughts?
|
| « Last Edit: Oct 17th, 2007, 5:13pm by Pietro K.C. » |
 IP Logged IP Logged |
"I always wondered about the meaning of life. So I looked it up in the dictionary under 'L' and there it was --- the meaning of life. It was not what I expected." (Dogbert)
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Calculus of variations
« Reply #6 on: Oct 17th, 2007, 7:03pm » |
 Quote Quote  Modify Modify
|
on Oct 17th, 2007, 5:11pm, Pietro K.C. wrote:
You can try a simpler approach using Euler's formula.
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Pietro K.C.
Full Member
  

 

Gender: 
Posts: 213
|
 |
Re: Calculus of variations
« Reply #7 on: Oct 17th, 2007, 9:57pm » |
 Quote Quote  Modify Modify
|
Quote:| You can try a simpler approach using Euler's formula |
|
Is that the one in Euler's theorem? 
I'm kidding.  But this solution by symmetry is one of those things which I just haven't sat down to work out fully, even though I have a hunch it might work. But this solution by symmetry is one of those things which I just haven't sat down to work out fully, even though I have a hunch it might work.
One nice feature of the method is that it gives you existence of a maximum area together with one maximizing curve. I think some finer analysis of the symmetrization might even yield uniqueness.
|
|
 IP Logged IP Logged |
"I always wondered about the meaning of life. So I looked it up in the dictionary under 'L' and there it was --- the meaning of life. It was not what I expected." (Dogbert)
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register