 Author
Author |
Topic: harmonic (Read 4671 times) |
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
What is 1-1/2 +1/3 -1/4...
what about 1/9 +1/19+1/29...(all that have a nine anywhere in the denominator)
|
|
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: harmonic
« Reply #1 on: Oct 1st, 2007, 8:43pm » |
 Quote Quote  Modify Modify
|
First is 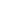 (1) (1) 
Second is complemented depleted/Kempner series.
|
| « Last Edit: Oct 1st, 2007, 8:52pm by Sameer » |
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: harmonic
« Reply #2 on: Oct 1st, 2007, 9:06pm » |
 Quote Quote  Modify Modify
|
I meant what are their numerical values.
|
|
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: harmonic
« Reply #3 on: Oct 1st, 2007, 9:19pm » |
 Quote Quote  Modify Modify
|
on Oct 1st, 2007, 9:06pm, srn347 wrote:| I meant what are their numerical values. |
|
First one is another way of saying what is its numerical value!! That's the way how we do it!!
For second I would say 80 http://www.qbyte.org/puzzles/p072s.html
|
| « Last Edit: Oct 1st, 2007, 9:48pm by Sameer » |
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: harmonic
« Reply #4 on: Oct 1st, 2007, 9:24pm » |
 Quote Quote  Modify Modify
|
The n thing doesn't tell me the number. the 80 was on the right track, but out of the loop(the track shouldn't be shaped like a loop anyway). Go back to line 10(in binary).
|
|
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: harmonic
« Reply #5 on: Oct 1st, 2007, 9:42pm » |
 Quote Quote  Modify Modify
|
on Oct 1st, 2007, 9:24pm, srn347 wrote:| The n thing doesn't tell me the number |
|
It does if you know Dirichlet!!
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: harmonic
« Reply #6 on: Oct 2nd, 2007, 6:28am » |
 Quote Quote  Modify Modify
|
was that supposed to be the remnien zeta? regardless, I require an actual answer.
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: harmonic
« Reply #7 on: Oct 2nd, 2007, 6:50am » |
 Quote Quote  Modify Modify
|
on Oct 2nd, 2007, 6:28am, srn347 wrote:| was that supposed to be the remnien zeta? regardless, I require an actual answer. |
|
Not many people write eta when they mean zeta. Sameer's answer is correct: the Dirichlet Eta function evaluated at 1.
|
|
 IP Logged IP Logged |
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: harmonic
« Reply #8 on: Oct 2nd, 2007, 7:21am » |
 Quote Quote  Modify Modify
|
Nope. I don't know how you got an answer of 1...
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: harmonic
« Reply #9 on: Oct 2nd, 2007, 7:26am » |
 Quote Quote  Modify Modify
|
on Oct 2nd, 2007, 7:21am, srn347 wrote:| Nope. I don't know how you got an answer of 1... |
|
He doesn't, he gets eta(1).
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: harmonic
« Reply #10 on: Oct 2nd, 2007, 7:27am » |
 Quote Quote  Modify Modify
|
The Dirichlet Eta function evaluated at 1 evaluates as ln(2).
|
| « Last Edit: Oct 2nd, 2007, 7:27am by Grimbal » |
 IP Logged IP Logged |
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: harmonic
« Reply #11 on: Oct 2nd, 2007, 7:27am » |
 Quote Quote  Modify Modify
|
Does that mean zeta 1? That is incorrect.
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: harmonic
« Reply #12 on: Oct 2nd, 2007, 7:28am » |
 Quote Quote  Modify Modify
|
on Oct 2nd, 2007, 7:27am, srn347 wrote:| Does that mean zeta 1? That is incorrect. |
|
No, it means exactly what it says.
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: harmonic
« Reply #13 on: Oct 2nd, 2007, 10:06am » |
 Quote Quote  Modify Modify
|
347, your series 1 - 1/2 + 1/3 - 1/4 +..... = loge2 = 0.63452380952380952380952380952381...
Edit: loge2 = 0.69314718055994530941723212145818...
|
| « Last Edit: Oct 3rd, 2007, 9:40am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: harmonic
« Reply #14 on: Oct 2nd, 2007, 4:32pm » |
 Quote Quote  Modify Modify
|
Nope. there is fallacy in your statement.
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: harmonic
« Reply #15 on: Oct 2nd, 2007, 4:40pm » |
 Quote Quote  Modify Modify
|
on Oct 2nd, 2007, 4:32pm, srn347 wrote:| Nope. there is fallacy in your statement. |
|
Until "loge2", ThudanBlunder is correct (although you may be more familiar with seeing it written as ln 2), but I don't know where he got his decimal expression. Maple tells me it's 0.693147180559945309417232121458176568...
By the way, also eta(1) = ln 2.
|
| « Last Edit: Oct 2nd, 2007, 4:52pm by pex » |
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: harmonic
« Reply #16 on: Oct 2nd, 2007, 5:02pm » |
 Quote Quote  Modify Modify
|
Just for completeness, the second series diverges. Proof:
Its "complement", the series summing the reciprocals of all integers containing no nines, is
(1/1 + 1/2 + ... + 1/8)
+ (1/10 + 1/11 + ... + 1/18 + 1/20 + ... + 1/88)
+ (1/100 + ... + 1/888)
+ ...
The n-th bracketed term contains 8*9n-1 numbers which are reciprocals of n-digit integers. Thus, the sum is less than
8*(1/1) + 8*9*(1/10) + 8*92*(1/100) + ...
= 8*sum{n=0 to infinity} (9/10)n
= 8 * 1/(1-9/10) = 80,
which means that it converges.
We know that the sum of reciprocals of all integers (1/1 + 1/2 + 1/3 + ...) diverges, and we know that the sum of the reciprocals of all integers that contain no nines converges. This means that the part that is left over, the sum of the reciprocals of all integers that do contain nines, must diverge.
|
| « Last Edit: Oct 2nd, 2007, 5:03pm by pex » |
 IP Logged IP Logged |
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: harmonic
« Reply #17 on: Oct 2nd, 2007, 8:46pm » |
 Quote Quote  Modify Modify
|
It is not log or ln of whatever. should I tell you what it is?
|
|
 IP Logged IP Logged |
|
|
|
Obob
Senior Riddler
   

Gender: 
Posts: 489
|
 |
Re: harmonic
« Reply #18 on: Oct 2nd, 2007, 10:19pm » |
 Quote Quote  Modify Modify
|
Its very arrogant of you to tell all these people who are much smarter than you that they are wrong. Especially since they are in fact correct, and you don't even know the math involved.
|
|
 IP Logged IP Logged |
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: harmonic
« Reply #19 on: Oct 2nd, 2007, 11:38pm » |
 Quote Quote  Modify Modify
|
The first one is zero, because it is the harmonic series(infinity) minus itself. 1-1/2+1/3...=1-(1-1/2)+1/3-(1/2-1/4)...=(1-1)+(1/2-1/2)+(1/3)-1/3... If you think it's arrogant, try taking ritalin. if you are offended, blame the one whom the phase originated from.
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: harmonic
« Reply #20 on: Oct 3rd, 2007, 12:40am » |
 Quote Quote  Modify Modify
|
on Oct 2nd, 2007, 11:38pm, srn347 wrote:| The first one is zero, because it is the harmonic series(infinity) minus itself. 1-1/2+1/3...=1-(1-1/2)+1/3-(1/2-1/4)...=(1-1)+(1/2-1/2)+(1/3)-1/3... If you think it's arrogant, try taking ritalin. if you are offended, blame the one whom the phase originated from. |
|
Wow. This could just be one of the most stupid things I've ever seen.
One. "Infinity minus infinity" is not well-defined; by no means does it have to be zero.
Two. You are trying to use the commutative property (look it up) of addition in a conditionally convergent series (look that one up too). This generally does not work.
Three. Any decent textbook or website that treats limits will tell you that the value is ln 2.
Four. So did multiple math-inclined (to say the least) people above.
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: harmonic
« Reply #21 on: Oct 3rd, 2007, 2:25am » |
 Quote Quote  Modify Modify
|
Five. Try the start of the sequence on your trusty calculator, and you'll see that in no way does it tend to 0.
Six. Ritalin does not work against other people's arrogance, so no matter how much ritalin any of us were to take, you'd still be an arrogant little bugger.
|
| « Last Edit: Oct 3rd, 2007, 2:26am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: harmonic
« Reply #22 on: Oct 3rd, 2007, 6:55am » |
 Quote Quote  Modify Modify
|
Try solving the second series.
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: harmonic
« Reply #23 on: Oct 3rd, 2007, 7:20am » |
 Quote Quote  Modify Modify
|
on Oct 3rd, 2007, 6:55am, srn347 wrote:| Try solving the second series. |
|
Look further up in the thread - it diverges. But you're not going to believe this anyway.
Edit: perhaps it's nice if I mention that "my" proof of this fact was inspired rather heavily by NickH's solution in the link Sameer posted. Night-time plagiarism...
|
| « Last Edit: Oct 3rd, 2007, 7:25am by pex » |
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: harmonic
« Reply #24 on: Oct 3rd, 2007, 7:58am » |
 Quote Quote  Modify Modify
|
*sigh* how come you didn't tell us you didn't want the solution that everyone knows but the one that you concocted up... it would have made our thinking so much simpler than these god knows what eta, zeta, etc..
Edit: I tried giving benefit of doubt and encouraging good posts, but it seems it is pointless.
|
| « Last Edit: Oct 3rd, 2007, 8:04am by Sameer » |
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register