 Author
Author |
Topic: Summation (Read 1231 times) |
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
Let F(n) = 2n + 2/3 - en (k - n)ke-k/k! for k = 0 to n-1 and n = 1,2,3,4,....... (k - n)ke-k/k! for k = 0 to n-1 and n = 1,2,3,4,.......
a) Prove that F(n) 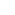 0 as n 0 as n 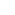 
b) Find F(1000) to 3 significant figures.
c) Find the smallest m such that |F(m)| < |F(m+1)|
|
| « Last Edit: Sep 10th, 2007, 1:43pm by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Summation
« Reply #1 on: Sep 10th, 2007, 5:43pm » |
 Quote Quote  Modify Modify
|
The poor convergence makes me think Poisson summation would be in order.
Anyway, let f(n,k) = (n-k)k e-k/k!. We want to approximate  (-1)k f(n,k). (-1)k f(n,k).
For fixed n, f(n,k) is maximized when
f(n,k+1) ~ f(n,k), or (n-k-1)k+1/(k+1) ~ e(n-k)k.
Letting k =  n, we want n, we want
(1 - 1/[n(1- )]) )]) n(n-k-1)/(k+1) ~ e. n(n-k-1)/(k+1) ~ e.
Letting n   , we get , we get
e- /(1- /(1- ) (1- ) (1- )/ )/ = e = e
which is to say,  /(1- /(1- ) = ) =  = W(1/e) ~ 0.2785, or = W(1/e) ~ 0.2785, or  ~ 0.2178. ~ 0.2178.
Now, the maximum value is about f(n,  n) ~ e n) ~ e n/ n/ {2 {2  n}. n}.
Plotting f(n, k), it looks like a constant times normal, with mean  n, and variance ~ n, and variance ~ 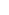 n, where n, where 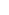 ~ 0.1332? (I don't know what ~ 0.1332? (I don't know what 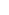 is.) That is, f(n,k) ~ C N( is.) That is, f(n,k) ~ C N( n, n, 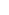 n). Considering the max, e n). Considering the max, e n/ n/ {2 {2  n} = C/ n} = C/ {2 {2 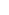 n}, so C = e n}, so C = e n n  { {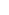 / / }. Or, in other words, }. Or, in other words,
gn(x) = f(n, kx) ~ e n/n n/n  { {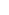 / / } N( } N( , , 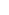 /n), /n),
and we are interested in  (-1)k gn(k/n). But I don't think this is a good enough approximation. It looks pretty lousy, actually. Eh. (-1)k gn(k/n). But I don't think this is a good enough approximation. It looks pretty lousy, actually. Eh.
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Summation
« Reply #2 on: Sep 10th, 2007, 6:38pm » |
 Quote Quote  Modify Modify
|
I'm guessing it has something to do with
 01 en cos( 01 en cos( nx) (1/x - 1)nx (2 nx) (1/x - 1)nx (2 nx)-1/2 dx. nx)-1/2 dx.
It seems to converge to 1, but it's a bit tricky to approximate.
|
| « Last Edit: Sep 10th, 2007, 8:29pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Summation
« Reply #3 on: Sep 11th, 2007, 2:35pm » |
 Quote Quote  Modify Modify
|
This might be useful: define
f(x) =  k<x (-1)k (x-k)k ex-k/k!. k<x (-1)k (x-k)k ex-k/k!.
This looks a lot like some sort of generating function. So look at
f'(x) =  (-1)kex-k/k! { (x-k)k + k(x-k)k-1 } = f(x) + (-1)kex-k/k! { (x-k)k + k(x-k)k-1 } = f(x) +  (-1)kex-k/(k-1)! (x-k)k-1 (-1)kex-k/(k-1)! (x-k)k-1
= f(x) -  (-1)rex-1-r/r! (x-1-r)r (-1)rex-1-r/r! (x-1-r)r
= f(x) - f(x-1)
So f'(x) = f(x) - f(x-1), or f' =  f, where f, where  is the difference operator. That is, the slope of the tangent at each point is the same as the secant going one back. Interesting. is the difference operator. That is, the slope of the tangent at each point is the same as the secant going one back. Interesting.
So f'= f, with f(x)=ex for x in [0,1], and we want to show f(x) ~ 2x + 2/3. But I've never been very good with differential equations. f, with f(x)=ex for x in [0,1], and we want to show f(x) ~ 2x + 2/3. But I've never been very good with differential equations.
Integrating f'= f, from 1 to x, gives f, from 1 to x, gives
f(x) - f(1) =  x-1x f(t)dt - x-1x f(t)dt -  01 f(t)dt, 01 f(t)dt,
or
f(x) = 1 +  x-1x f(t)dt. x-1x f(t)dt.
I don't know if that helps either.
|
| « Last Edit: Sep 11th, 2007, 2:43pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Summation
« Reply #4 on: Sep 11th, 2007, 3:27pm » |
 Quote Quote  Modify Modify
|
Well, I can show one thing. Intuitively, since f' =  f, f should straighten out to be close to linear. So suppose f'(x) f, f should straighten out to be close to linear. So suppose f'(x)  c. We show c=2. c. We show c=2.
For x>0, and t>0, set
gx(t) = [f(x+t) - f(x)]/t = f'(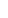 ) )
for some 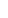 in [x, x+t], by the intermediate value theorem. By assumption then, gx(t) = c + hx(t), where hx converges to 0, uniformly in t, as x in [x, x+t], by the intermediate value theorem. By assumption then, gx(t) = c + hx(t), where hx converges to 0, uniformly in t, as x   . Now, . Now,
f(x+t) = f(x) + tc + thx(t),
and so
f(x) + c + hx(1) = f(x+1)
= 1 +  01 f(x+t)dt 01 f(x+t)dt
= 1 + f(x) + c/2 +  01 thx(t)dt. 01 thx(t)dt.
Letting x  gives c=2. gives c=2.
[f(x) is not actually differentiable everywhere, but if you read the next post, it suffices to work with G(x) = F(x) - x2, which is differentiable. So if we can show that g = G' converges to a constant, then that constant must be 2/3, and the result follows.]
|
| « Last Edit: Sep 11th, 2007, 7:30pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Summation
« Reply #5 on: Sep 11th, 2007, 4:03pm » |
 Quote Quote  Modify Modify
|
Aha, but we can repeat the argument!
Let g(x) = f(x) - 2x. Then g satisfies the same differential equation: g' =  g, and the integral equation becomes g, and the integral equation becomes
g(x) =  x-1x g(t)dt. x-1x g(t)dt.
Now, let G be an antiderivative of g. Then the above becomes G' =  G, and so as before G, and so as before
G(x) = G(1) -  01 G(t)dt + 01 G(t)dt +  x-1x G(t)dt x-1x G(t)dt
= 1/3 +  x-1x G(t)dt, x-1x G(t)dt,
since G(x) = ex - x2 on [0,1]. The same argument as for f now gives G(x) ~ 2/3 x + c'. Which is to say, g ~ 2/3, and finally f(x) ~ 2x + 2/3.
So all we need to prove is: suppose g(x) =  x-1x g(t)dt. Then g(x) converges to a finite value, namely x-1x g(t)dt. Then g(x) converges to a finite value, namely
2 01 [ g(t) - 01 [ g(t) -  0t g(u)du ] dt. 0t g(u)du ] dt.
Intuitively, this is much more clear than the original problem: g(x) is simply the average of g(t) over [x-1,x]. How could it possibly not converge 
|
| « Last Edit: Sep 11th, 2007, 4:34pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Summation
« Reply #6 on: Sep 11th, 2007, 4:26pm » |
 Quote Quote  Modify Modify
|
The last term in F(n) looks very similar to a Discrete(?) Laplace transform!! F(s) = Integral f(t)*e-st dt
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Summation
« Reply #7 on: Sep 11th, 2007, 4:57pm » |
 Quote Quote  Modify Modify
|
Laplace!!
Let fk(t) = (t-k)ket-k/k!, when t>k, and 0 otherwise. Then the Laplace transform works out to be
Fk(s) =  k k fk(t) e-st dt fk(t) e-st dt
= e-ks/(s-1)k+1,
and the Laplace transform of f(t) =  (-1)kfk(t) is the sum of the geometric series (-1)kfk(t) is the sum of the geometric series
F(s) =  (-1)kFk(s) (-1)kFk(s)
= 1/(s-1+e-s)
= 2/s2 + 2/(3s) + 1/18 - s/270 + ...
= 2/s2 + 2/(3s) + G(s).
Inverse Laplacing,
f(t) = 2t + 2/3 + g(t),
and presumably g(t)  0. G(s) is meromorphic, with infinitely many poles, at each non-zero solution to e-s=1-s: 0. G(s) is meromorphic, with infinitely many poles, at each non-zero solution to e-s=1-s:
s = -log(a+ ) )  (a- (a- )i, a=2 )i, a=2 k+ k+ /2, /2,  ~ (1+log a)/a, ~ (1+log a)/a,  ~ [(log a)2-1]/2a, k ~ [(log a)2-1]/2a, k   +, +,
all in the left half-plane. But I'm not familiar enough with the Laplace transform to know how g(t) behaves.
|
| « Last Edit: Sep 11th, 2007, 5:48pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Summation
« Reply #8 on: Sep 11th, 2007, 5:12pm » |
 Quote Quote  Modify Modify
|
For G(s) you get s in the numerator ? That will make the system unstable and non-convergent!!! I will take a closer look when I get home!! ? That will make the system unstable and non-convergent!!! I will take a closer look when I get home!!
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Summation
« Reply #9 on: Sep 11th, 2007, 6:59pm » |
 Quote Quote  Modify Modify
|
g(t) =1/(2 ) )  - -  G(iu)eiutdu, G(iu)eiutdu,
which is essentially the Fourier transform of G(iu). G(iu) isn't in L1, so the above isn't actually integrable, and we can't use the Riemann-Lebesgue lemma, but since G(iu) is in L2 and analytic, I think it follows that g(t) goes to 0, decaying exponentially in fact.
Actually, we are only interested in
Re g(t) = 1/(2 ) )  [Re G(iu) cos(ut) - Im G(iu) sin(ut)]dt, [Re G(iu) cos(ut) - Im G(iu) sin(ut)]dt,
and Re G(iu) is in L1, since Re[1/(iu-1+e-iu)] ~ (cos u - 1)/u2, and Re[2/(iu)2 + 2/(3iu)] = -2/u2.
So the only issue is whether  Im G(iu)sin(ut)dt goes to 0. Im G(iu)sin(ut)dt goes to 0.
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
Whahahaha:
Recapitulating,
G(z) = 1/(z-1+e-z) +2/(3z) - 2/z2,
and we want to compute, for t>0,
g(t) = 1/(2 i) i)  -i -i i i G(z)eztdz. G(z)eztdz.
Fix M>0, and let N>0 be large. Consider the rectangular contour going from -iM  iM iM  -N+iM -N+iM  -N-iM -N-iM  -iM. The integral along the right edge is what we want to evaluate. Waving my hands, the integral along the other three sides should be small. This just leaves the residues inside the rectangle. -iM. The integral along the right edge is what we want to evaluate. Waving my hands, the integral along the other three sides should be small. This just leaves the residues inside the rectangle.
G(z)ezt has a pole at z=c, where e-c=1-c. The residue there is
limz->c (z-c)G(z)ezt = ect / limz->c (z-1+e-z)/(z-c)
= ect / (1 - e-c )
= ect / c.
Now the poles come in conjugate pairs, and adding up the residues inside the rectangle, and letting M go to infinity, we get:
g(t) =  c 2Re[ ect/c ] (*) c 2Re[ ect/c ] (*)
where the sum is over conjugate pairs of non-zero c satisfying e-c=1-c. That is,
c = {-2.09  7.46 I, -2.66 7.46 I, -2.66  13.9 I, -3.03 13.9 I, -3.03  20.22 I, -3.29 20.22 I, -3.29  26.54 I, ...} 26.54 I, ...}
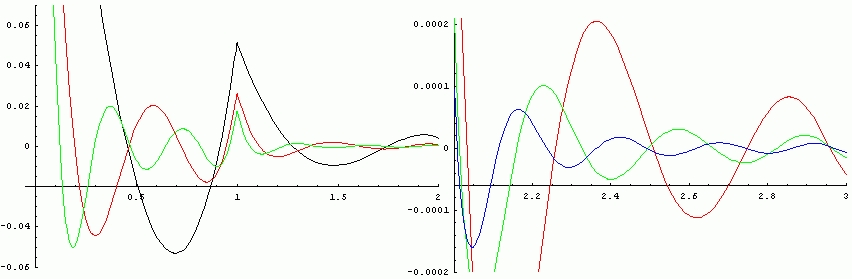
Let gn(t) be the sum of the first n terms of the Fourier series (*), and let hn(t) = f(t) - 2t - 2/3 - gn(t). Attached are plots of g=h0, h1, h2, and h3, in black, red, green, and blue, respectively. (Only h1,h2 are shown in both.) Hooray Fourier series! Finally,
-F(1000) = g(1000) = 2Re[e1000c1/c1 + e1000c2/c2 + ...]
= 1.1469767*10-909 - O(10-1158).
Note that this makes sense: the functions y(x)=x, y(x)=1, and y(x)=ecx, where c=1-e-c, are all solutions to y'(x) = y(x) - y(x-1), and f(x) is a linear combination of these:
f(x) = 2x + 2/3 +  ecx/c. ecx/c.
~ 2x + 2/3 + 0.258*e-2.089 x cos(7.461 x + 1.298) + O(e-2.664 x).
And it appears n=800 is the first time |F(n)| < |F(n+1)|.
|
| « Last Edit: Sep 12th, 2007, 7:41am by Eigenray » |
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Summation
« Reply #11 on: Sep 12th, 2007, 7:15pm » |
 Quote Quote  Modify Modify
|
Another problem that involved Fourier transform was Alternating Sum: as z  1-, 1-,
S(z) =  k=0 k=0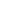 (-1)k z2^k (-1)k z2^k
= 1/2 - (1-z)/3 + g(z) + 2/log 2  {m>0 odd} Re[ {m>0 odd} Re[  (m (m i/log 2)ex m i/log 2)ex m i ], i ],
where z = e-2^(-x), and g(z) = O((1-z)2).
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Summation
« Reply #12 on: Sep 12th, 2007, 9:08pm » |
 Quote Quote  Modify Modify
|
What's your solution, T&B?
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Summation
« Reply #13 on: Sep 14th, 2007, 4:33pm » |
 Quote Quote  Modify Modify
|
on Sep 12th, 2007, 9:08pm, Barukh wrote:| What's your solution, T&B? |
|
Although I did elementary Complex Variable at uni, it was a long time ago and I have forgotten most of it. (However, this does not stop me knowing a good problem when I see one.) So I won't write out the full solution as though I am a real mathematician like Eigenray.
But 'my' solution begins by letting
I(n,x) =  (k-n)ke(k-n)x/k! = (k-n)ke(k-n)x/k! =  Dk(1/k!)e(k-n)x/Dxk between k = 0 and n Dk(1/k!)e(k-n)x/Dxk between k = 0 and n
Thus F(n) = 2n + 2/3 - I(n,-1)
As e(k-n)x is an entire function in the complex plane we are now able to apply Cauchy's Theorem to prove that
F(n) = 2n + 2/3 -  (1/2 (1/2 i) i)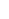 e(k-n)x/(1+z)k+1.dz e(k-n)x/(1+z)k+1.dz
where the contour integral must enclose z = -1, and sum over k explicitly.
Further details on request, but I believe Eigenray will be able to see the rest of this method for a)
(I wish the edit window wasn't so small and that we could save drafts of our work, so as not to lose it somehow before posting.)
|
| « Last Edit: Sep 16th, 2007, 11:02am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Summation
« Reply #14 on: Sep 15th, 2007, 9:49am » |
 Quote Quote  Modify Modify
|
I will type my solution up in MathType as soon as I have time.
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Summation
« Reply #15 on: Sep 15th, 2007, 5:15pm » |
 Quote Quote  Modify Modify
|
Summing the (finite) geometric series, we get
F(n) = 2n + 2/3 + 1/(2 i) i) 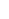 (1+z+ez)-1/(1+z)n dz, (1+z+ez)-1/(1+z)n dz,
since e-nz/(1+z-ez) is analytic at z=-1. So by Cauchy's theorem, we get
1/(1+z-ez) =  n=1 n=1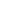 [F(n) - 2n - 2/3] (z+1)n-1, [F(n) - 2n - 2/3] (z+1)n-1,
and killing the pole at 0,
G(z) = 1/(1+z-ez) - 2/(3z) + 2/z2
=  F(n) (z+1)n-1. F(n) (z+1)n-1.
It took me a while to realize that this actually proves (a)! Hint: where are the poles of G? Amazing. Complex analysis just seems a little too beautiful sometimes.
Now for (b) (and to get the Fourier series) we just play "Whac-A-Pole".
on Sep 14th, 2007, 4:33pm, ThudanBlunder wrote:| (I wish the edit window wasn't so small and that we could save drafts of our work, so as not to lose it somehow before posting.) |
|
Yes. Unfortunately the textarea width and height are set in css, so something like TextareaResize doesn't work. I couldn't even resize it using DOM Inspector, but there's probably a way. Googling around, I put together the following, which seems to work okay:
Code:
var resizetextarea=function() {
var a = Math.max(350, window.innerWidth*0.70 - 150);
GM_addStyle("textarea{ width: "+a+"px !important; }");
}
resizetextarea();
window.addEventListener('resize', function() {resizetextarea(); }, true); |
|
I just stuck it inside SMQ's Greasemonkey script. Of course you can modify the parameters I used, and add something similar for height. But I don't know much about this sort of thing; there should be a way to just remove the width and height styles, so that modifying the rows and cols attributes will work.
Edit: Textarea_drag_resize works nicely. But it could be customized to default to some affine function of the window's width and height.
|
| « Last Edit: Sep 15th, 2007, 11:31pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Summation
« Reply #16 on: Sep 16th, 2007, 9:52am » |
 Quote Quote  Modify Modify
|
on Sep 14th, 2007, 4:33pm, ThudanBlunder wrote:
Although I did elementary Complex Variable at uni, |
|
... and I haven't done it at all. That's not good.
Eigenray, could you please elaborate on your "too beautiful" solution?
Also, is there good material to read on the subject?
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Summation
« Reply #17 on: Sep 16th, 2007, 2:43pm » |
 Quote Quote  Modify Modify
|
on Sep 16th, 2007, 9:52am, Barukh wrote:| Eigenray, could you please elaborate on your "too beautiful" solution? |
|
Use the fact that the radius of convergence of a power series is the distance to the nearest singularity.
Quote:| Also, is there good material to read on the subject? |
|
Have a look at Generatingfunctionology, particularly section 5.2 (and section 2.4 for background). The basic tool for all this is Cauchy's Integral Formula.
I know Stein & Shakarchi's Complex Analysis has a chapter on asymptotics, but I don't have my copy on me. Googling on some keywords (complex analysis, generating functions, asymptotics) also turns up this, apparently part of the book Analytic Combinatorics, which seems pretty comprehensive.
|
| « Last Edit: Sep 16th, 2007, 4:28pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Summation
« Reply #18 on: Sep 16th, 2007, 3:07pm » |
 Quote Quote  Modify Modify
|
on Sep 16th, 2007, 9:52am, Barukh wrote:
... and I haven't done it at all. That's not good.
Also, is there good material to read on the subject?
|
|
My Engineering Math text book used to have all this. Yet it has been a long time!! Maybe any Higher Engineering Mathematics should have this!! I should look for one too!! hmm...
|
| « Last Edit: Sep 16th, 2007, 3:07pm by Sameer » |
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register