Author |
Topic: Factoring large numbers is easy (Read 2982 times) |
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender: 
Posts: 1948
|
 |
Factoring large numbers is easy
« on: May 31st, 2007, 12:52pm » |
 Quote  Modify
|
(1) Suppose you are given a function sqrt(a,n), which returns an integer b such that b2  a mod n, if it exists. Give an efficient algorithm to factor n.
(2) Suppose you are given a function order(a,n), which returns the smallest positive integer k for which ak 1 mod n. Give an efficient algorithm to factor n.
|
|
 IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Factoring large numbers is easy
« Reply #1 on: Jun 22nd, 2007, 4:31am » |
Quote Modify
|
For the (1), take a to be a perfect square - that's the basic idea of Dixon's factorization algorithm.
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Factoring large numbers is easy
« Reply #3 on: Jul 24th, 2007, 2:02pm » |
Quote Modify
|
Hint (sort of): In 1994, Peter Shor discovered that ord(a,n) can actually be computed (with arbitrarily small error probability) in polynomial time ... on a quantum computer.
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Factoring large numbers is easy
« Reply #4 on: Jul 27th, 2007, 1:56am » |
Quote Modify
|
Uh?! This "hint" actually gives away the whole solution.
So simple...
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Factoring large numbers is easy
« Reply #5 on: Jul 27th, 2007, 6:12am » |
Quote Modify
|
Well, it was a hint in the sense that it tells you what to look up if you want to look it up. Note that it is similar to part (1), in that you are using the period to find a random square root of 1.
But the Wikipedia entry is missing a key point:
Quote:| If N also does not divide (ar/2+1), then N must have a nontrivial common factor with each of (ar/2-1) and (ar/2+1). |
|
What is the probability that this happens, if we pick a at random? This requires a bit of number theory, and is the reason I put this problem in the putnam section.
In particular, prove that this algorithm does in fact find a non-trivial factor of N with probability > 1- , in time polynomial in log(N).
|
| « Last Edit: Jul 27th, 2007, 6:17am by Eigenray » |
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Factoring large numbers is easy
« Reply #6 on: Jul 30th, 2007, 3:22am » |
Quote Modify
|
Quote:| If N also does not divide (ar/2+1)… |
|
on Jul 27th, 2007, 6:12am, Eigenray wrote:| What is the probability that this happens, if we pick a at random? |
|
I will consider the case N = pq, p, q odd prime numbers, here.
I will use the following notations:
ordp(a) – multiplicative order of a modulo p;
T(x) – maximum power of 2 dividing x (i.e. x = 2T(x)d, d an odd number).
Let T(p-1) = n > 0. I am going to divide the numbers 1, …, p-1 into n+1 classes 0, 1, …, n s.t. number a belongs to class k iff T(ordp(a)) = k.
Let g be a primitive root modulo p. Then, a = gs for some s < p. Let’s count the numbers s with T(s) = k. Consider two cases:
1. k  n, then T(ordp(a)) = n-k (why?), and there are (p-1)/2k+1 of these.
2. k > n. Then T(ordp(a)) = 0, and there are (p-1)/ 2n+1 of these.
In any case, the number of elements in class k doesn’t exceed p/2.
Getting back to N = pq: If N divides ar/2+1, that means both p, q divide it. That is, p, q both divide ar-1, but not ar/2-1. Therefore, T(ordp(a)) = T(ordq(a)).
Picking a at random modulo N, let’s fix k = T(ordp(a)). Then, the probability that T(ordq(a)) = k won’t exceed 1/2.
So, the number that leads to a non-trivial factor is chosen with probability > 1/2.
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Factoring large numbers is easy
« Reply #7 on: Jul 30th, 2007, 5:16am » |
Quote Modify
|
Exactly. The argument generalizes easily to any odd N, since ZN* = C1 x ... x Cr is a product of cyclic groups is all that is used.
In fact, we can compute the probability of failure exactly: given that a is relatively prime to N, the algorithm fails exactly when T(|a1|) = ... T(|ar|) = t, for some t, where |ai| represents the order of a projected into the cyclic group Ci. When t=0, the probability of this is
 1/2Ti,
where Ti = T(|Ci|). For 0 < t m = min(T1,...,Tr), the probability is
1/2Ti-t+1.
Altogether, the probability of failure is
P = 2-S[1 + (2rm-1)/(2r-1)] = [2rm + 2r - 2]/[2S(2r-1)]
where S= Ti. Since S  rm r, we have
P [2rm + 2r - 2]/[2rm(2r-1)] 1/2r-1.
Of course, the algorithm fails when r=1.
|
|
IP Logged |
|
|
|
Benny
Uberpuzzler
Gender:
Posts: 1024
|
|
Re: Factoring large numbers is easy
« Reply #8 on: Feb 20th, 2008, 1:57pm » |
Quote Modify
|
Eigenray wrote:
(1) Suppose you are given a function sqrt(a,n), which returns an integer b such that b^2 = a mod n, if it exists. Give an efficient algorithm to factor n.
..................................
I use a theorem which is derived from the one below.
Theorem:
For any positive integer N, suppose there exists an integer A such that
A^x=1(modN) for some integer x. If q is a prime divisor of x such that A^(x/q) =/= 1(modN),
and if there exists a prime divisor p of N, such that q does not divide p-1, then
GCD(A^(x/q) -1(modN), N) =/= 1
Can you prove the above
So basically if we were to find k(=order(a,n)), and q is some prime divisor of k (if k is prime than we can just divide it by itself), then the above thereom says that as long as there exists a prime divisor p of n such that q=/=p-1, then gcd(A^(x/q) -1(modn), n) will give us a nontrivial factor of n.
|
|
IP Logged |
If we want to understand our world — or how to change it — we must first understand the rational choices that shape it.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Factoring large numbers is easy
« Reply #9 on: Feb 20th, 2008, 3:20pm » |
Quote Modify
|
on Feb 20th, 2008, 1:57pm, BenVitale wrote:For any positive integer N, suppose there exists an integer A such that
A^x=1(modN) for some integer x. If q is a prime divisor of x such that A^(x/q) =/= 1(modN),
and if there exists a prime divisor p of N, such that q does not divide p-1, then
GCD(A^(x/q) -1(modN), N) =/= 1
Can you prove the above |
|
Yes. Suppose p | N but GCD(Ax/q-1, N) = 1. Then Ax/q 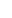 1 mod p. Since Ax = 1 mod p, it follows that Ax/q mod p has order q, and therefore q | p-1.
Quote:| So basically if we were to find k(=order(a,n)), and q is some prime divisor of k (if k is prime than we can just divide it by itself), then the above thereom says that as long as there exists a prime divisor p of n such that q=/=p-1, then gcd(A^(x/q) -1(modn), n) will give us a nontrivial factor of n. |
|
But consider for example n=85. For any A relatively prime to n, k=order(A,n) is a power of 2, but all prime divisors of n are 1 mod 2. So gcd(Ak/2-1, n) is not guaranteed to be non-trivial. Of course there's still a good chance that it is, but not because of that theorem.
|
|
IP Logged |
|
|
|
Benny
Uberpuzzler
Gender:
Posts: 1024
|
|
Re: Factoring large numbers is easy
« Reply #10 on: Feb 20th, 2008, 9:04pm » |
Quote Modify
|
Eigenray,
The theorem doesn't apply to this example because 2 divides p-1 for every prime factor p of 85.
Remember, we only have that gcd(A^k/q - 1, n) nontrivial if there exists at least one prime factor p
of n such that q=\=p-1. In your example, there are none.
Note: Situations like your example are very rare. Most often we can always find numbers that will
satisfy the conditions of the theorem (and even if we can't, its still likely that gcd(A^k/2 - 1, n)
will be nontrivial anyway). Quote: Quote: Quote:
|
|
IP Logged |
If we want to understand our world — or how to change it — we must first understand the rational choices that shape it.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Factoring large numbers is easy
« Reply #11 on: Feb 20th, 2008, 9:49pm » |
Quote Modify
|
on Feb 20th, 2008, 9:04pm, BenVitale wrote:| The theorem doesn't apply to this example |
|
Yes, that was my point. I was demonstrating why the theorem doesn't prove that your algorithm will always work.
If you click the 'quote' link, the message text box should start out with text that looks like:
[quote author=... ]Text to quote
[/quote]
Then just write your reply after the [/quote] tag (you can also trim the text between the tags to include only what you're replying to).
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print