Author |
Topic: Rank of Redheffer Matrix (Read 1253 times) |
|
Aryabhatta
Uberpuzzler
Gender: 
Posts: 1321
|
 |
Rank of Redheffer Matrix
« on: Apr 11th, 2007, 4:54pm » |
 Quote  Modify
|
Let RHn be the nxn RedHeffer matrix defined as:
RHn(i,j) = 1 if i divides j or j = 1
RHn(i,j) = 0 otherwise.
For instance RH4 is
[1 1 1 1]
[1 1 0 1]
[1 0 1 0]
[1 0 0 1]
Prove that the rank of RHn is atleast n-1.
|
| « Last Edit: Apr 11th, 2007, 5:51pm by Aryabhatta » |
 IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Rank of Redheffer Matrix
« Reply #1 on: Apr 11th, 2007, 6:48pm » |
Quote Modify
|
The lower-right (n-1)x(n-1) submatrix is upper unitriangular.
2) Show that
det(RHn) =  k=1n  (k).
Hence RHn is invertible except for
n=2, 39, 40, 58, 65, 93, ....
3) Is the above set infinite?
|
|
IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
Gender:
Posts: 1321
|
|
Re: Rank of Redheffer Matrix
« Reply #2 on: Apr 12th, 2007, 12:39am » |
Quote Modify
|
on Apr 11th, 2007, 6:48pm, Eigenray wrote:
3) Is the above set infinite? |
|
Is this known?
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
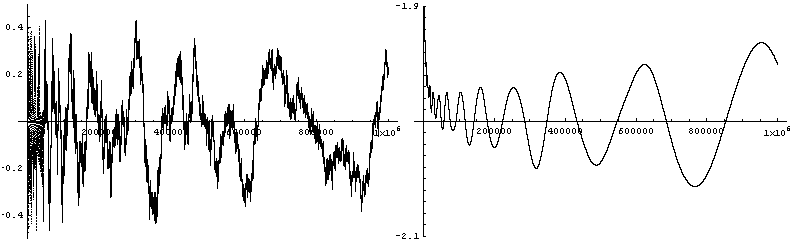
No idea. You'd think they would say one way or the other on Mathworld, but Sloane usually says when a sequence is not known to be infinite.
It seems likely though. Here's a graph of M(n)/ n. It looks roughly like a random walk.
But it's not as a random as it looks -- on the right is a graph of A(A(A(M))), where
A(F)(n) = 1/n k=1n F(k)
is the averaging operator. The position of the n-th maxima fits Ce.45 n pretty well.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print