Author |
Topic: Limit Problem (Read 460 times) |
|
ThudnBlunder
Uberpuzzler
The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
|
|
 IP Logged |
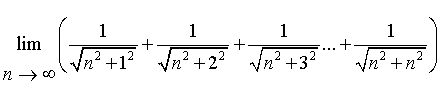
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
 |
Re: Limit Problem
« Reply #1 on: Jan 4th, 2007, 2:30am » |
 Quote  Modify
|
Taking an integration as approximation of the summation, I get
LN(sqrt(2) + 1)
Not entirely sure whether they are the same in the limit though.
|
| « Last Edit: Jan 4th, 2007, 2:31am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Limit Problem
« Reply #2 on: Jan 4th, 2007, 7:11pm » |
Quote Modify
|
If we pull a factor of 1/n out of all terms, what we have is (1/n)(f(1/n) + f(2/n) + f(3/n) + ... + f(n/n)), where f(x) = 1/sqrt(1+x2). This is a Cauchy sum for f for the interval [0,1]. Hence it's limit is the integral of f(x) over that interval, provided the integral exists. Since f(x) = d/dx(arcsinh x), the limit is as towr gave.
|
| « Last Edit: Jan 4th, 2007, 7:12pm by Icarus » |
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print