 Author
Author |
Topic: Another Limit Problem (Read 768 times) |
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|

|
|
 IP Logged IP Logged |
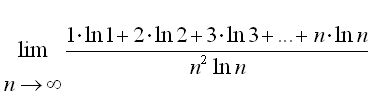
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Another Limit Problem
« Reply #1 on: Jan 4th, 2007, 3:30am » |
 Quote Quote  Modify Modify
|
0.49...?
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Another Limit Problem
« Reply #2 on: Jan 4th, 2007, 7:28pm » |
 Quote Quote  Modify Modify
|
As with the other limit problem, this one can be reduced by means of a Cauchy sum, though it is trickier to pull it off. Subtract out and then add back in (n(n+1)/2) ln n to the numerator. The result can be expressed as
(1/n)(f(1/n) + f(2/n) + ... + f(n/n))/(n ln n) + (n+1)ln n/2n ln n, where f(x) = x ln x
The numerator of the first fraction is the Cauchy sum for f(x) on [0,1], and since f is continuous and bounded on this interval, the integral exists and is finite. Since the denominator is unbounded, the entire fraction goes to zero. The final term obviously has limit 1/2, and therefore so does the entire expression.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Another Limit Problem
« Reply #3 on: Jan 5th, 2007, 4:58am » |
 Quote Quote  Modify Modify
|
Alternatively, let F(n) =  1n xln(x) dx. Then, for every finite n, the numerator of the given expression is bounded from above and from below by F(n+1) and F(n). 1n xln(x) dx. Then, for every finite n, the numerator of the given expression is bounded from above and from below by F(n+1) and F(n).
|
|
 IP Logged IP Logged |
|
|
|
JP05
Guest

|
Question: Barukh, how did you get that integral symbol in that post? If there is supposed to be a toolbar with that symbol I am not seeing it.
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Another Limit Problem
« Reply #5 on: Jan 5th, 2007, 4:14pm » |
 Quote Quote  Modify Modify
|
on Jan 5th, 2007, 3:38pm, JP05 wrote:| Question: Barukh, how did you get that integral symbol in that post? If there is supposed to be a toolbar with that symbol I am not seeing it. |
|
You can click on the Quote link of any post to see how it was written.
There used to be a drop-down menu of maths symbols but it is not functional at the moment.
|
| « Last Edit: Jan 5th, 2007, 4:17pm by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
JP05
Guest

|
Oh! I did not know quote would expose what some typed but it does, thanks. Not having a list of named symbol file names make this hard. From the looks of what I see with quote you can include a symbol file from any http source (right?).
|
|
 IP Logged IP Logged |
|
|
|
balakrishnan
Junior Member
 

Gender: 
Posts: 92
|
 |
Re: Another Limit Problem
« Reply #7 on: Jan 5th, 2007, 5:30pm » |
 Quote Quote  Modify Modify
|
It is 1/2
Just follows from the fact that the numerator
~ int[x*log(x)]_{x=0 to n}
which is n^2/2*log(n)+O(n^2)
and hence the limit is 1/2
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Another Limit Problem
« Reply #8 on: Jan 5th, 2007, 7:38pm » |
 Quote Quote  Modify Modify
|
on Jan 5th, 2007, 4:36pm, JP05 wrote:| Oh! I did not know quote would expose what some typed but it does, thanks. Not having a list of named symbol file names make this hard. From the looks of what I see with quote you can include a symbol file from any http source (right?). |
|
You can use the image tags [ img ] [ /img ] to post an image from anywhere (these are actually available from one of those buttons above the smileys on the reply page - I suggest going through all the buttons to see what they do. Some of them can be useful). The math symbolry we used to have is still available in the directory http://www.ocf.berkeley.edu/~wwu/YaBBImages/symbols/. By following that link, you can see the directory contents - though its hard to figure out what the individual gifs are from their names. William had a really nice system set up for using these images as smileys. But unfortunately, he had to upgrade the version of YaBB that the forum runs under, and all his customizations disappeared. While he has restored - and improved - the other customizations, this one never got fixed.
There is a thread in the Suggestions forum (near the top, as it is sticky) on how to display mathematical symbols. If you read the entire thread, you can see a glimpse of the history of this forum. But what is useful starts with this post. In particular, in the post after mine, SMQ gives a wonderful script that allows Firefox users to see pages written with the old symbolry in all their glory! If you would like the see the posts I created to start off the 0.999... thread in the Medium forum as they are supposed to look, download Firefox and GreaseMonkey if you haven't already, and install this script. (They were so pretty, and now I can't even redo them as the max size of a post has decreased, and they are too big to modify.  ) )
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register