Author |
Topic: Overlapping Circle and Triangle (Read 3745 times) |
|
ThudnBlunder
Uberpuzzler
The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
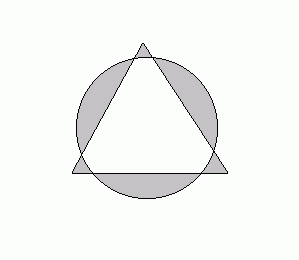
An equilateral triangle of unit side length overlaps a circle of radius r centred at the centre of the triangle. What value of r will minimize the shaded area in the diagram?
|
|
 IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
 |
Re: Overlapping Circle and Triangle
« Reply #1 on: Dec 14th, 2006, 3:47am » |
 Quote  Modify
|
Possibly, it's 1/3 . But after all the problems I encountered in my calculation, I'm not sure of anything at the moment.
|
| « Last Edit: Dec 14th, 2006, 3:47am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Overlapping Circle and Triangle
« Reply #2 on: Dec 14th, 2006, 5:47am » |
Quote Modify
|
I would say the same on the simple principle that the proportion of circle inside the triangle must be 1/2. When it is the case the increase of area outside the triangle matches the decrease of area inside the triangle when the radius increases infinitesimally. Geometrically you find a diameter of 2/3.
|
| « Last Edit: Dec 14th, 2006, 7:51am by Grimbal » |
IP Logged |
|
|
|
ThudnBlunder
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
Well done, Grimbal. An astute observation. As usual toiling towr is also right. 
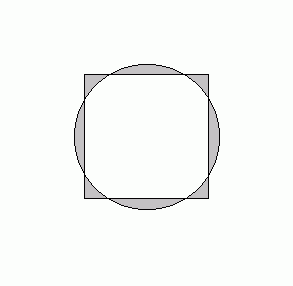
How about if we replace the triangle with a square?
With a regular n-gon?
|
| « Last Edit: Dec 14th, 2006, 7:10am by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Overlapping Circle and Triangle
« Reply #4 on: Dec 14th, 2006, 8:48am » |
Quote Modify
|
In general I get sqrt(2) cot( [pi] /n)/[2 sqrt(cos( [pi] /n) + 1)]
for larger n it's approximately n/(2 [pi]) ; or better yet n/(2 [pi]) - 1/( [pi]n)
|
| « Last Edit: Dec 14th, 2006, 9:06am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
ThudnBlunder
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Overlapping Circle and Triangle
« Reply #5 on: Dec 14th, 2006, 12:34pm » |
Quote Modify
|
That's right, towr!
Slightly simpler is (1/2)*cot(pi/n)sec(pi/2n)
How did you get your 1/n(pi) refinement?
Also, the optimal circle has equal arc lengths inside and outside of the n-gon for all n.
|
| « Last Edit: Dec 15th, 2006, 1:04pm by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Overlapping Circle and Triangle
« Reply #6 on: Dec 14th, 2006, 12:49pm » |
Quote Modify
|
on Dec 14th, 2006, 12:34pm, THUDandBLUNDER wrote:| How did you get your 1/n(pi) refinement? |
|
I guessed 
I plotted the difference and saw a hyperbola, and I tried a few values, pi seemed a nice one to leave it at.
Possibly a taylor series could find a better justified fit.
|
| « Last Edit: Dec 14th, 2006, 12:51pm by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Overlapping Circle and Triangle
« Reply #7 on: Dec 14th, 2006, 10:05pm » |
Quote Modify
|
You would expect r ~ n/(2pi) since the circumference ~ n. In fact,
r = n/(2pi) - 5pi/(48 n) - 293pi3/(11520 n3) - ...
But lets flip it around: fix the radius of the circle at 1, and vary the polygon. Then the inradius is
r = cos(pi/2n) = [1+cos(pi/n)]/2,
and if R is the circumradius, then
rR = [1+sec(pi/n)]/2,
and the area is
A = n[tan(pi/n) + sin(pi/n)]/2.
|
| « Last Edit: Dec 14th, 2006, 10:30pm by Eigenray » |
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print