Author |
Topic: Alternating Sum (Read 1735 times) |
|
ThudnBlunder
Uberpuzzler
The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Alternating Sum
« on: Aug 24th, 2006, 4:09am » |
 Quote  Modify
|
For 0 < x < 1, consider S(x) = x - x2 + x4 - x8 + x16 - x32 +... - ...
Does S(x) tend to a limit as x -> 1 from below, and if so what is this limit?
|
| « Last Edit: Aug 24th, 2006, 10:18am by ThudnBlunder » |
 IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Sameer
Uberpuzzler
Pie = pi * e
Gender:
Posts: 1261
|
|
Re: Alternating Sum
« Reply #1 on: Aug 24th, 2006, 3:39pm » |
Quote Modify
|
EVEN if I know the answer the ODDs are that somebody will post a nice solution so I will waitS(x) is an oscillating series as it approaches 1
|
| « Last Edit: Aug 24th, 2006, 3:42pm by Sameer » |
IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Alternating Sum
« Reply #2 on: Aug 24th, 2006, 6:52pm » |
Quote Modify
|
Coming up with the value isn't hard. Showing that S converges to it (I'm fairly certain it does) is another matter.
By Hadamard's formula, the series converges to an analytic S for all |x| < 1. Note also that S(x) = x - S(x2), whereby it is clear that S(1-) = 1/2, if it exists at all.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Sameer
Uberpuzzler
Pie = pi * e
Gender:
Posts: 1261
|
|
Re: Alternating Sum
« Reply #3 on: Aug 24th, 2006, 11:27pm » |
Quote Modify
|
what about S(1+) ? Doesn't that tell if S converges if x->1
|
|
IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Alternating Sum
« Reply #4 on: Aug 25th, 2006, 6:38am » |
Quote Modify
|
on Aug 24th, 2006, 11:27pm, Sameer wrote:| what about S(1+) ? Doesn't that tell if S converges if x->1 |
|
The series for S(x) doesn't converge if x>1. And S(z) can't be analytically continued outside the unit disk, so there's no other way to sensibly define S(x), x>1. But that doesn't really matter, since the question is only asking about the limit from the left.
|
|
IP Logged |
|
|
|
Sameer
Uberpuzzler
Pie = pi * e
Gender:
Posts: 1261
|
|
Re: Alternating Sum
« Reply #5 on: Aug 25th, 2006, 9:42am » |
Quote Modify
|
Ah ok I misinterpreted x->1 from below!! Thanks for clarifying..
|
|
IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Alternating Sum
« Reply #6 on: Aug 25th, 2006, 5:25pm » |
Quote Modify
|
Here is one way to show that it converges (though I leave the nasty details where the devil hides out):
Let C(x) be the Cesaro sum of the series: If Sn(x) = x - x2 + ... - x2^(n-1), then C = limn (1/n)(S1 + S2 + ... + Sn).
The following facts hold:
1) If a sequence converges, then the Cesaro sum converges to the same limit.
2) C(1) converges to 1/2.
3) (the nasty part) C(1-) = C(1).
4) by (1), S(1-) = C(1-) = C(1).
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Deedlit
Senior Riddler
Posts: 476
|
|
Re: Alternating Sum
« Reply #7 on: Aug 25th, 2006, 10:02pm » |
Quote Modify
|
S(x) = x / (1+x) for -1 < x < 1, and lim [x -> 1-] x / (1 + x) = 1/2. 
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Alternating Sum
« Reply #8 on: Aug 26th, 2006, 12:15am » |
Quote Modify
|
on Aug 25th, 2006, 10:02pm, Deedlit wrote:| S(x) = x / (1+x) for -1 < x < 1, and lim [x -> 1-] x / (1 + x) = 1/2. |
|
Isn't it true for S'(x) = x - x2 + x3 - x4 + ... ?
|
|
IP Logged |
|
|
|
Deedlit
Senior Riddler
Posts: 476
|
|
Re: Alternating Sum
« Reply #9 on: Aug 26th, 2006, 1:53am » |
Quote Modify
|
Heh heh. Today is just one of those days...
|
|
IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: Alternating Sum
« Reply #10 on: Aug 26th, 2006, 10:39am » |
Quote Modify
|
You can spot an easy functional relationship between S(x) and S(x^2);
then let x -> 1- and you'll arrive at the same result. I think most
things about this function are proved from that functional relationship.
|
| « Last Edit: Aug 26th, 2006, 10:44am by Michael Dagg » |
IP Logged |
Regards,
Michael Dagg
|
|
|
Sameer
Uberpuzzler
Pie = pi * e
Gender:
Posts: 1261
|
|
Re: Alternating Sum
« Reply #11 on: Aug 26th, 2006, 11:40am » |
Quote Modify
|
S(x) = x - S(x2)
So let's compute S(x2) first
S(x2) = x2 - x4 + x8 ..
sum of series formula
S(x2) = x2/(1+x2)
So S(x) = x - x2/(1+x2)
Computing x->1- gives 1/2
Did I miss anything?
|
| « Last Edit: Aug 26th, 2006, 11:40am by Sameer » |
IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Alternating Sum
« Reply #12 on: Aug 26th, 2006, 12:14pm » |
Quote Modify
|
x2/(1+x2) = x2 - x4 + x6 - x8 + ...
S(x2) = x2/(1+x2) = x2 - x4 + x8 - x16 + ...
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: Alternating Sum
« Reply #13 on: Aug 26th, 2006, 12:16pm » |
Quote Modify
|
Alternatively, see if you can come up with a g(x) and h(x) such
that you can squeeze it: g(x) <= S(x) <= h(x)
|
| « Last Edit: Aug 26th, 2006, 12:16pm by Michael Dagg » |
IP Logged |
Regards,
Michael Dagg
|
|
|
Sameer
Uberpuzzler
Pie = pi * e
Gender:
Posts: 1261
|
|
Re: Alternating Sum
« Reply #14 on: Aug 26th, 2006, 12:27pm » |
Quote Modify
|
on Aug 26th, 2006, 12:14pm, Icarus wrote:x2/(1+x2) = x2 - x4 + x6 - x8 + ...
S(x2) = x2/(1+x2) = x2 - x4 + x8 - x16 + ... |
|
ugh.. i knew it came too easy and so had to be some problem... ok I think I need lunch to think this over!! Thanks Icarus for pointing this out..
|
|
IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
ThudnBlunder
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Alternating Sum
« Reply #15 on: Aug 26th, 2006, 1:07pm » |
Quote Modify
|
on Aug 26th, 2006, 12:27pm, Sameer wrote:| ok I think I need lunch to think this over!! |
|
S(x4) = ?
|
|
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
on Aug 25th, 2006, 5:25pm, Icarus wrote:
The following facts hold: |
|
By the process of elimination...
Quote:| 3) (the nasty part) C(1-) = C(1). |
|
...are you sure about that?
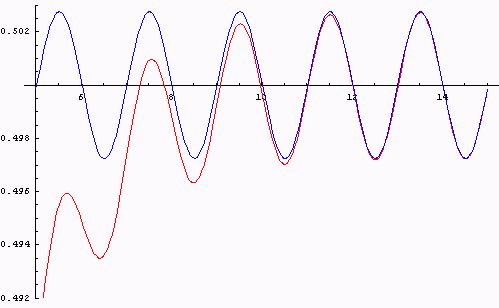
Attached is a graph of S(e-2^-x) (in red).
Following Exercise 5, by Poisson summation, for A>1, and z = e-2^-x,
 (-A)nz2^n = 1/log 2 Gamma((log A - (2n-1)pi i)/log 2)ex(log A - (2n-1)pi i),
where the sum is over all integers n. I don't see how to let A->1, because when A=1, the sum on the left doesn't converge (as n->-infinity). But, when z -> 1 (x->infinity), the sum for negative n is "-A/(1+A)-ish", which does go to -1/2, so in some sense
S(z) = n>=0 z2^n ~* 1/2 + 1/log 2 Gamma(-(2n-1)pi i/log 2)e-(2n-1)pi i x
= 1/2 + 2/log 2 Re[ Gamma(pi i/log 2)epi i x + Gamma(3pi i/log 2)e3pi i x + ... ].
Gamma(iy) decays exponentially as y->infinity; compare S(z) (red) to F1(x) (blue):
F1(x) = 1/2 + 2/log 2 Re[ Gamma(pi i/log 2)epi i x ]
= 1/2 + 2/log 2 |Gamma(pi i/log 2)|cos(pi x + Arg Gamma(pi i/log 2)).
Arg Gamma(pi i/log 2) ~ .48 pi, so this is why S(z)=1/2 for x close to an integer.
*Anybody know how to make this precise?
|
| « Last Edit: Sep 12th, 2007, 6:58pm by Eigenray » |
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Alternating Sum
« Reply #17 on: Aug 26th, 2006, 2:20pm » |
Quote Modify
|
My previous post notwithstanding, there is in fact an elementary solution to the original question, though you'll quite likely need to use a computer to show the existence of an x with S(x)>1/2.
Followup: show that S(z) doesn't extend continuously to any connected open set intersecting the unit circle.
Harder: do any radial limits exist?
|
|
IP Logged |
|
|
|
ThudnBlunder
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Alternating Sum
« Reply #18 on: Aug 26th, 2006, 3:08pm » |
Quote Modify
|
on Aug 26th, 2006, 12:27pm, Sameer wrote:| ok I think I need lunch to think this over!! |
|
Looks like someone stole your thunder, Sameer! 
|
|
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Alternating Sum
« Reply #19 on: Aug 26th, 2006, 3:38pm » |
Quote Modify
|
on Aug 25th, 2006, 5:25pm, Icarus wrote:The following facts hold:
1) If a sequence converges, then the Cesaro sum converges to the same limit. |
|
But we want the reverse, don't we?
A Cesaro sum might converge if the original sequence doesn't.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Sameer
Uberpuzzler
Pie = pi * e
Gender:
Posts: 1261
|
|
Re: Alternating Sum
« Reply #20 on: Aug 26th, 2006, 6:01pm » |
Quote Modify
|
on Aug 26th, 2006, 3:08pm, THUDandBLUNDER wrote:
Looks like someone stole your thunder, Sameer! |
|
Yes, most definitely especially this being some of the things I studied as math in my electrical engineering... my eyes lit up with something in putnam i can try my hand at!! .. most of the questions in putnam go over my head!! 
|
| « Last Edit: Aug 26th, 2006, 6:02pm by Sameer » |
IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
ThudnBlunder
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Alternating Sum
« Reply #21 on: Aug 27th, 2006, 8:37am » |
Quote Modify
|
on Aug 26th, 2006, 6:01pm, Sameer wrote:
most of the questions in putnam go over my head!! |
|
In spite of Eigenray's admirable display of mathematical erudition, this is not one of them.
You can still solve this for yourself by noting that S(x) > S(x4) and S(0.995) > 1/2
|
| « Last Edit: Aug 27th, 2006, 8:37am by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Alternating Sum
« Reply #22 on: Aug 27th, 2006, 2:00pm » |
Quote Modify
|
on Aug 26th, 2006, 3:38pm, towr wrote:
But we want the reverse, don't we?
A Cesaro sum might converge if the original sequence doesn't.
|
|
It is somewhat pointless now, since that Eigenray and T&B want to be such poor sports about it as to disprove my claim of (3)  , but had (3) been true, it would have been sufficient.
The problem, if the answer were positive, would not require the series for S to converge at 1, only that the limits S(x) themselves converge as x --> 1-. Since S(x) = C(x) for x < 1, this is the same as saying C(x) converges as x --> 1-.
I went this way because Cesaro sums converge much more easily than regular limits, and are usually more stable. Further, I had already established that the limit of S, if it existed, was the Cesaro sum of the series for x=1.
Alas, there really was a devil hiding in those details, as Eigenray and Thud&Blunder have made clear. 
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Alternating Sum
« Reply #23 on: Aug 27th, 2006, 11:24pm » |
Quote Modify
|
Eigenray, how did you get these graphs?
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Alternating Sum
« Reply #24 on: Aug 28th, 2006, 2:14pm » |
Quote Modify
|
In[1]:=S[z_]= Sum[(-1)^n z^(2^n), {n,0,Infinity}];
F[x_,n_]= 2/Log[2] Re[Sum[Gamma[(2k-1)Pi I/Log[2]] E^((2k-1)Pi I x), {k,1,n}]];
Plot[{S[E^(-2^(-x))], 1/2+F[x,1]}, {x,5,15}, PlotRange->{.492,.503}, AxesOrigin->{5,.5}, PlotStyle->{{RGBColor[1,0,0]}, {RGBColor[0,0,1]}}]
or some such.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print