Author |
Topic: differential control system. (Read 1534 times) |
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
differential control system.
« on: Mar 28th, 2005, 7:32am » |
 Quote  Modify
|
This shouldn't be hard at all, but is nevertheless proving impossible for me..
given
dx/dt = 2x(t)+u(t), x(0)=x_0
Find the optimal function u(t) which minimizes u(t)^2, such that x(1)=0
I keep getting u(t)=0, which is obviously wrong seeing as x gets pushed away from the origin when there's no input.
|
|
 IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
|
Re: differential control system.
« Reply #1 on: Mar 28th, 2005, 10:25am » |
Quote Modify
|
on Mar 28th, 2005, 7:32am, towr wrote:
Find the optimal function u(t) which minimizes u(t)^2, such that x(1)=0
|
|
By minimizing u2(t), do you mean minimizing the quadratic integral \int_0^\infty u2(t) dt ? Or do you mean L-infinity norm?
|
|
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: differential control system.
« Reply #2 on: Mar 28th, 2005, 10:34am » |
Quote Modify
|
on Mar 28th, 2005, 10:25am, william wu wrote:
By minimizing u2(t), do you mean minimizing the quadratic integral \int_0^\infty u2(t) dt ? Or do you mean L-infinity norm? |
|
I mean \int_0^1 u2(t) dt
The point is to get from x(0)=x_0 in t=0 to x(1)=0 in t=1, with a little energy as possible.
|
| « Last Edit: Mar 28th, 2005, 10:37am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
|
Re: differential control system.
« Reply #3 on: Mar 28th, 2005, 12:26pm » |
Quote Modify
|
Well, I can solve the problem if x(0) = 0 and x(1) = xdes (steer zero intial condition to nonzero condition). Then the solution is:
u(tau) = (4 xdes) ( e2(1-tau)) / (e4 - 1 ) for 0 <= tau <= 1
Does that help? At first I thought if I can solve it this way, I should be able to use this to solve the reverse problem. Maybe someone else knows how to use it.
I tried just doing a naive translation of the system, y = x - xe, but this results in a nonlinear differential equation: ydot = 2x + u = 2y + 2xe + u.
|
| « Last Edit: Mar 28th, 2005, 12:37pm by william wu » |
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: differential control system.
« Reply #4 on: Mar 28th, 2005, 12:49pm » |
Quote Modify
|
Nope, the reverse course doesn't help. Because x is pushed from the origin anyway.
It has soemthing to do with the hamiltonian
H(x,p,u) = p(2x + u) +1/2 (u^2)
which needs to be minimized
So
2px + pu +1/2 (u^2)
=
2px + 1/2 (u + p)^2 - 1/2p^2
Which is minimized wrt u if u=-p
-- the rest is speculation, and may be way off --
So we're left to minimize 2px-1/2p^2 wrt p and x
Now according to the book
I get
dp/dt = -2p, p(1)=x(1)=0 (?)
dx/dt = 2x - p, x(0)=1
but that would make p(t) = C*e^-2t, but C must be 0 if it's ever to reach p(1)=0. But this also makes p(t)=0 and thus u(t)=0. Which is proposterous..
|
| « Last Edit: Mar 28th, 2005, 12:51pm by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
just ignored your most recent post for the time being 
Is there a way to determine what the minimum energy of the optimal input should be, without determining the input yet?
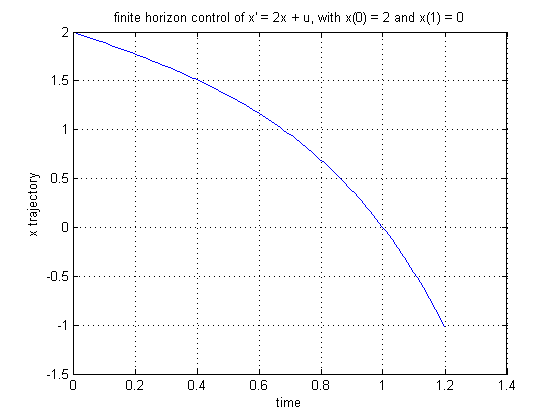
Stubbornly sticking with my reverse strategy, here's an input that works, in the sense that it meets the target:
u(tau) = - 2xe + 4(-xe)*(e2(1 - tau) )/(e4 - 1)
(After translating the system to the origin, I designed an input that cancels the nonlinearity to get a nonlinear system, then applied the solution for the reverse problem. Whether it is minimum energy though, I don't know. Probably not.)
Attached an image in case the curve shape tells you anything:
|
| « Last Edit: Mar 28th, 2005, 1:20pm by william wu » |
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: differential control system.
« Reply #6 on: Mar 28th, 2005, 1:58pm » |
Quote Modify
|
I think
p = c exp(-2t)
x = 1/4 c exp(-2t) + a exp(2t)
with
a = 1-1/4 c
c = 1/ (1-exp(-4))
might give the solution
But I'm too tired to check it now.. (also still, u=-p)
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: differential control system.
« Reply #7 on: Mar 29th, 2005, 4:39am » |
Quote Modify
|
Hopefully the full solution.
problem description
dx/dt = 2x(t)+u(t), x(0)=x_0, x(1)=0
minimizing \int_0^1 u(t)^2 dt
The Hamiltonian
(note that p functions as langrange multiplier)
H(x,p,u) = p(2x + u) +1/2 (u^2)
= 2px + 1/2 (u + p)^2 - 1/2p^2
=> u = -p
From H by construction
dx/dt = dH/dp = 2x + u = 2x - p
dp/dt = -dH/dx = -2p
solving the new differential equations
dp/dt = -dH/dx = -2p
=>
p = c*exp(-2t)
dx/dt = 2x - p
=>
x = k(t) exp(2t)
using variation of constants
dx/dt = k'(t) exp(2t) + 2 k(t) exp(2t)
dx/dt = 2x - p = 2 k(t) exp(2t) - c*exp(-2t) {from before}
k'(t) exp(2t) = - c*exp(-2t)
k'(t) = - c*exp(-4t)
k(t) = 1/4 c*exp(-4t) + k
x(t) = k(t) exp(2t) = 1/4 c*exp(-2t) + k exp(2t)
Using the boundary conditions
x(0) = x_0 = 1/4 c + k
=> k = x_0 - 1/4 c
x(1) = 0 = 1/4 c*exp(-2) + k exp(2)
=> k = - 1/4 c*exp(-4)
x_0 - 1/4 c = - 1/4 c*exp(-4)
=> c = 4 x_0 / (1- exp(-4))
k= - exp(-4) x_0 / (1- exp(-4)) = x_0 / (1 - exp(4))
(barring mistakes) The solution
x_opt(t) = x_0 * [exp(-2t) / (1 - exp(-4)) + exp(2t) / (1 - exp(4)) ]
p_opt(t) = x_0 * exp(-2t) / (1 - exp(-4))
u_opt(t) = - x_0 * exp(-2t) / (1 - exp(-4))
Follow up question:
Given matrices A and B, assuming the system (A,B) is controllable, solve
dx/dt = Ax(t)+Bu(t), x(0)=x_0, x(1)=0
minimizing \int_0^1 u^T(t)u(t) dt = \int_0^1 ||u(t)||^2 dt
Where x \in R^n and u \in R^m (and the matrices have the appropriate dimensions as well)
[Which is the real problem I was struggling with last night..]
|
| « Last Edit: Mar 29th, 2005, 4:54am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print