Author |
Topic: covering a curve (Read 1730 times) |
|
JocK
Uberpuzzler
Gender: 
Posts: 877
|
 |
covering a curve
« on: Dec 14th, 2004, 1:39pm » |
 Quote  Modify
|
Prove or disprove that any continuous planar curve of length 5/2 can be fully covered by a simple convex shape of area unity.
|
| « Last Edit: Dec 15th, 2004, 12:11pm by JocK » |
 IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: covering a curve
« Reply #1 on: Dec 18th, 2004, 10:49am » |
Quote Modify
|
This is a "heuristic proof" (i.e. it has a bunch of hand-waving rather than solid logic), but I think it can be cleaned up to make a real proof:
For any such curve, the boundary of it's convex hull is the union of a shorter curve and a line segment, so if all convex regions whose boundaries consist of a curve of length <= 5/2 and a line segment have area <= 1, the problem is solved. The closed curve of this form with maximal area is a semi-circle. The radius of the semi-circle is 5/2[pi], and the area is 25/8[pi] [approx] 0.9947.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
Disclaimer: This is a kind of off-topic, since it describes a different problem.
Icarus was right by picking a semi-circle as a cover. The “solid proof” goes as follows.
It is clear that for any curve we may pick a point S on it and draw a line l through this point such that every point of the curve lies in the same half-plane with l as a boundary. Let’s call l the support line.
1. If the curve is closed, it cannot extend more than the length 5/4 in any direction. Then, the semi-circle with radius 5/4 centered at S on the support line covers the curve.
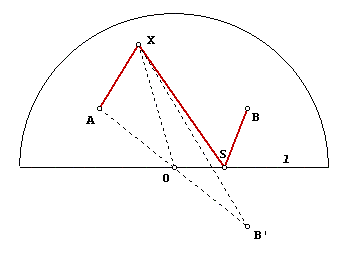
2. If the curve is not closed, let A, B be its endpoints (see attached figure). Let l be a support line parallel to the line AB. Let X be any point on the curve between points A and S. Reflect point B in l to get B’, and let O be the intersection of AB’ with l. Now we can use the fact that the length of the median of the triangle is less than the average of the lengths of 2 adjacent sides to derive
OX [le] (XA+XB’)/2 [le] (AX+XS+SB)/2 [le] 5/4
Exactly in the same manner it is shown that OX [le] 5/4 when X lies between points S and B. Therefore, the semi-circle centered at O with radius 5/4 on line l covers every curve of length 5/2.
The problem stated here is a special case of the so called Moser’s Worm Problem, which may be simply stated as follows:
What is the region of smallest area which will cover every planar curve of length 1?
As you may see, it’s still not solved. Jock’s proposed question shows that this area is less than 0.4. The proof presented here was proposed by A. Meir about 35 years ago.
|
| « Last Edit: Jan 2nd, 2005, 8:04am by Barukh » |
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: covering a curve
« Reply #3 on: Dec 22nd, 2004, 3:38pm » |
Quote Modify
|
Not quite the proof I had in mind, but it works, at least once the typo is corrected:
on Dec 22nd, 2004, 6:05am, Barukh wrote:| OX [le] (XA+XB’)/2 [le] (AX+XS+SB) [le] 5/4 |
|
This should be
OX [le] (XA+XB’)/2 [le] (AX+XS+SB)/2 [le] 5/4
I spent some time wondering why AX+XS+SB should be less than 5/4 before I realized the /2 had been inadvertently dropped.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: covering a curve
« Reply #4 on: Dec 23rd, 2004, 11:06pm » |
Quote Modify
|
on Dec 22nd, 2004, 3:38pm, Icarus wrote:This should be
OX [le] (XA+XB’)/2 [le] (AX+XS+SB)/2 [le] 5/4 |
|
Yes, of course! Thanks for pointing.
|
|
IP Logged |
|
|
|
JocK
Uberpuzzler
Gender:
Posts: 877
|
|
Re: covering a curve
« Reply #5 on: Jan 2nd, 2005, 7:20am » |
Quote Modify
|
on Dec 22nd, 2004, 6:05am, Barukh wrote:| Therefore, the semi-circle centered at O with radius 5/4 on line l covers every curve of length 5/2. |
|
A semi-circle with radius 5/4 has area exceeding unity. I don't think we are talking about the same problem here!
on Dec 22nd, 2004, 6:05am, Barukh wrote:The problem stated here is a special case of the so called Moser’s Worm Problem, which may be simply stated as follows:
What is the region of smallest area which will cover every planar curve of length 1?
As you may see, it’s still not solved. Jock’s proposed question shows that this area is less than 0.4. |
|
Maybe the problem was stated in a way that is somewhat ambigious, but I am not interested in the region of smallest area that covers every curve of given length. Rather, each curve can be covered by a different convex shape.
Btw: would this problem be a special case of Moser's Worm Problem, it would suggest a real breakthrough solution to Moser's Worm Problem of area less than 0.16. 
|
| « Last Edit: Jan 2nd, 2005, 7:21am by JocK » |
IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: covering a curve
« Reply #6 on: Jan 2nd, 2005, 8:02am » |
Quote Modify
|
on Jan 2nd, 2005, 7:20am, JocK wrote:| Maybe the problem was stated in a way that is somewhat ambigious, but I am not interested in the region of smallest area that covers every curve of given length. Rather, each curve can be covered by a different convex shape. |
|
Oops! You are right. Sorry for confusing everybody here.
But I think I'll leave the post for the reference - just delete a couple of wrong associations.
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: covering a curve
« Reply #7 on: Jan 21st, 2005, 3:34pm » |
Quote Modify
|
I've been thinking about this one, since it still lacks a proof. The method I see for proving this is a bit complicated to post in one or two posts, but I will outline it here. There is probably a simpler method, but this is the approach I see:
We operate in [bbr][sup2], and restrict attention to curves having the origin as one end point: Let M be the set of arc-length parametrized curves [gamma] with [gamma](0) = 0 and len([gamma]) = L for some fixed L (L=5/2 for this problem).
Lemma 1: M is complete under the uniform norm. [edit: this is false, but not necessary for the theorem]
(This requires arc-length parametrizations. Without this restriction, the sequences could converge uniformly to curves of any length, or even non-rectifiable curves)
Lemma 2: M is totally bounded (and therefore compact) under the uniform norm.
(This is probably the hardest part to prove. I am confident of it, however.)
For each [gamma] in M, define A([gamma]) = area of the convex hull of [gamma].
Lemma 4: A : M [to] [bbr] is continuous.
(It seems clear that it ought to be, but proving it could be tricky.)
The main consequence of these lemmas is:
Theorem 1: There exists a curve [gamma] in M for which A([gamma]) takes on its maximum value.
Proof: (Given the previous lemmas, this one is trivial). Since M is compact, so is A(M), and therefore it has a maximum A0. Choose any [gamma] in A-1(A0). [edit: the proof is more complicated, since the first lemma was false.]
Theorem 2: If [gamma] [in] M is not convex (i.e., is not contained within the boundary of its convex hull), then A([gamma]) < A0.
(The proof here involves flipping a section of the curve not on the boundary of the convex hull to point outward, thereby introducing additional area.)
Theorem 3: Among convex curves in M, The value of A is greatest for semi-circles.
(The calculus of variations should do for this.)
So any curve [gamma] in M has A([gamma]) less than or equal to that of a semicircle of length L, area = L2/2[pi].
For L = 5/2, this is 25/8[pi] [approx] 0.9947.
|
| « Last Edit: Jan 23rd, 2005, 1:47pm by Icarus » |
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: covering a curve
« Reply #8 on: Jan 22nd, 2005, 9:05am » |
Quote Modify
|
I have some time, so I thought I would get started on giving proofs of my lemmas.
Lemma 1: M is complete under the uniform norm.
Proof: Suppose an arbitrary sequence of arc-length parametrized curves {[gamma]n} defined on a fixed interval [0, [lambda]] converges uniformly to a map [gamma]. [gamma] is rectifiable with length d if d = sup{ [sum]i=1n |[gamma](xi) - [gamma](xi-1)| : n [in] [bbn] and {xi}i=0n an increasing sequence from [0, [lambda]]}.
Let {xi}i=0n be such sequence. Let [epsilon] > 0 and choose [delta] [in] {[gamma]k} such that ||[gamma] - [delta]|| < [epsilon]/2n. Then
[sum]i=1n |[gamma](xi) - [gamma](xi-1)| [le] [sum]i=1n |[gamma](xi) - [delta](xi)| + |[delta](xi) - [delta](xi-1)| + |[delta](xi-1) - [gamma](xi-1)|
[le] [sum]i=1n [epsilon]/2n + (xi - xi-1) + [epsilon]/2n [le] [epsilon] + [lambda].
Since [epsilon] was arbitrary, it must be that [sum]i=1n |[gamma](xi) - [gamma](xi-1)| [le] [lambda].
Therefore [gamma] is rectifiable with length [le] [lambda].
To show equality,...
At this stage it breaks down. What I had set out to prove turns out to be false. The restriction to arc-length parametrized curves is enough to guarantee that the limit is retifiable, and no longer than the converging curves, but that is all. It is quite possible for a sequence in M to converge to a shorter curve, or to a curve parametrized by something other than arc-length. (counter-example: Let [gamma]1(t) = (t/[surd]2, 1 - |1 - t/[surd]2|), for t [in] [0, 2[surd]2]. This curve is a sawtooth rising from the x-axis at x=0 and x=2 to peak at (1,1). Form each subsequent [gamma]i by flipping each tooth at 1/3 the distance from the axis to its peak or valley, so that the inner portion goes the other way:
/\
/ \
/ \
becomes
/\ /\
\/
These curves are all the same length and converge uniformly to the x-axis between 0 and 2, although this segment has just over 2/3 the common length of the sequence curves.)
So I am going to have to revamp my approach to prove the overall result in this fashion.
|
| « Last Edit: Jan 22nd, 2005, 9:22pm by Icarus » |
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: covering a curve
« Reply #9 on: Jan 23rd, 2005, 7:35pm » |
Quote Modify
|
The damage was not as bad as I thought. The same basic course still works, but I have to shuffle the pieces a bit.
Lemma 1: If a sequence of arc-length parametrized curves of length L converges uniformly, the limit curve is rectifiable with length [le] L.
(Proved in the previous post).
Lemma 2: M is totally bounded.
Proof: A set is totally bounded if for every [epsilon] > 0, it can be covered by a finite number of sets with diameter [le] [epsilon]. Note that every curve in M lies entirely within the closed disk of radius L about the origin. This disk is easily seen to be totally bounded. Let [call] be a finite collection of planar sets of diameter < [epsilon]/3 covering this disk. Also choose an integer N [ge] 3L/[epsilon], so L/N [le] [epsilon]/3. Since [call] is finite, there are only a finite number of distinct sequences S = {Si}i=0N [subseteq] [call]. For each such S define the set O(S) = {[gamma] [in] M : [gamma](iL/N) [in] Si for all i [le] N}. I claim that the diameter of O(S) [le] [epsilon].
Let [gamma], [delta] [in] O(S), and let x [in] [0, L]. Then for some i, iL/N [le] x [le](i+1)L/N. Therefore |x - iL/N| < [epsilon]/3. Also, both [gamma](iL/N) and [delta](iL/N) lie in the set Si, and so can be no farther than [epsilon]/3 apart. Since both [gamma] and [delta] are arc-length parametrizations,
|[gamma](x) - [delta](x)| [le] |[gamma](x) - [gamma](iL/N)| + |[gamma](iL/N) - [delta](iL/N)| + |[delta](iL/N) - [delta](x)|
< |x - iL/N| + [epsilon]/3 + |x - iL/N| [le] [epsilon].
So, ||[gamma] - [delta]|| [le] [epsilon], and thus the diameter of O(S) is [le] [epsilon].
Since [call] covers the disk, for any [gamma] in M, and for all i, [gamma](iL/N) must lie in some set Si [in] [call], and so [gamma] [in] O({Si}). Therefore the collection {O({Si}i=0N) : Si [in] [call]} is a finite collection of sets of diameter [le] [epsilon] that covers M. Thus M is totally bounded.
------------------
M is a subset of the space of all continuous curves in the plane. This space is known to be complete under the uniform norm. Let M' be the closure of M in this space. By Lemma 1, M' consists of rectifiable curves of length [le] L. Also, it is obvious that, just like M, [gamma](0) = 0 for all curves [gamma] in M'. Since M is totally bounded, so is M', and since M' is a closed subset of a complete space, M' is complete. Therefore M' is compact.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: covering a curve
« Reply #10 on: Jan 26th, 2005, 7:50pm » |
Quote Modify
|
I've had to make more changes in my original outline, but I finally have enough to prove the first theorem. Define the function A from all bounded curves in [bbr]2 to [bbr] so that A([gamma]) = the area of the convex hull of [gamma].
Lemma 4: A is upper-semicontinuous with respect to the uniform norm.
Proof: A is upper-semicontinuous at [gamma] if for every [epsilon] > 0, there is a [delta] > 0 such that if ||[gamma] - [alpha]|| < [delta], then A([alpha]) < A([gamma]) + [epsilon].
Let [epsilon] > 0. For any convex set B [subseteq] [bbr]2 and [delta] [ge] 0, define B([delta]) = { x : [exists] y [in] B with |x - y| [le] [delta] }. It is easy to see that B([delta]) is also convex. Somewhat harder to show, but still straight-forward is that as [delta] [to] 0, the area of B([delta]) converges to the area of B. In particular, if B is the convex hull of [gamma], then [exists] [delta] > 0 such that Area(B([delta])) < A([gamma]) + [epsilon]. For any curve [alpha] with ||[gamma] - [alpha]|| < [delta], since each point of [alpha] is within [delta] of a point on [gamma] within B, [alpha] [subset] B([delta]). And since B([delta]) is convex, the convex hull of [alpha] is also a subset of B([delta]). Therefore A([alpha]) [le] Area(B([delta])) < A([gamma]) + [epsilon]. So A is upper-semicontinuous.
One way of looking at upper-semicontinuity is that it is true continuity with respect to the upper-semi topology on [bbr]. The open sets of this topology are the interval (-[infty], x) for any x [in] [-[infty], [infty]]. It is easy to see that a non-empty set C [subseteq] [bbr] is compact if and only if C contains a maximum element: If C has a maximum z, then in any open cover, one of the sets (-[infty], x) must contain z. But then it must also contain anything less than z, including all of C. So this interval by itself constitutes a finite subcover, and C is compact. On the other hand, if C is unbounded, then {(-[infty], n) : n [in] [bbz]} is an open cover without a finite subcover. And if C is bounded without a maximum, then it has a supremum z not in C, and the collection {(-[infty], z - h) : h > 0} is an open cover without finite subcover.
Theorem 1: There exists [gamma] in M such that A([gamma]) is maximized on M.
Proof: Since M' is compact, and A is continuous under the upper-semi topology, A(M') is compact under that topology, and therefore contains a maximum value m. Let [gamma]' [in] A-1(m) [subseteq] M'. Since [gamma]' is in M', it has length [le] L. If its length were < L, then we could multiply [gamma]' by a constant to get another curve in M' with larger convex hull, so it must be that length([gamma]') = L. Let [gamma] be the arc-length parametrization of [gamma]'. Then [gamma] [in] M, and A([gamma]) = A([gamma]'), the maximum value of A on M' and M.
So, 1 theorem down, 2 more to go.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print