Author |
Topic: packing spheres inside a cube (Read 5903 times) |
|
JocK
Uberpuzzler
Gender: 
Posts: 877
|
 |
packing spheres inside a cube
« on: Aug 27th, 2004, 12:44pm » |
 Quote  Modify
|
What is the smallest number N of unit diameter spheres that can be packed inside a cube with volume V < N ?
|
|
 IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: packing spheres inside a cube
« Reply #1 on: Aug 28th, 2004, 9:09am » |
Quote Modify
|
It's a nice problem, Jock! I believe there is at least one relevant thread on the site.
Is 143 the right answer for the 2-D case? 
|
|
IP Logged |
|
|
|
JocK
Uberpuzzler
Gender:
Posts: 877
|
|
Re: packing spheres inside a cube
« Reply #2 on: Aug 28th, 2004, 12:14pm » |
Quote Modify
|
on Aug 28th, 2004, 9:09am, Barukh wrote:| Is 143 the right answer for the 2-D case? |
|
The answer for the 2-D case is certainly smaller than that. If I am not mistaken, one can pack 30 unit diameter circles inside a square of area 29.75.
(This follows from the fact that 6 rows of 5 touching spheres can be placed in a rectangle of size 5+x by 1+5[sqrt](1-x[sup2]), with 0 < x [le] 1/2. A square with approximate area 29.75 is obtained for x = (-4+5[sqrt]10)/26 [approx] 0.454284.)
|
| « Last Edit: Aug 28th, 2004, 2:08pm by JocK » |
IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: packing spheres inside a cube
« Reply #3 on: Aug 29th, 2004, 1:05am » |
Quote Modify
|
on Aug 28th, 2004, 12:14pm, JocK wrote:| The answer for the 2-D case is certainly smaller than that. If I am not mistaken, one can pack 30 unit diameter circles... |
|
.
Of course! My mistake was that I considered the densest circle packing only... 
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: packing spheres inside a cube
« Reply #4 on: Sep 2nd, 2004, 5:31am » |
Quote Modify
|
OK, for the original 3-D problem:
1. I have a fairly simple demonstration that N=63 may be arranged that way.
2. I have some evidence that N=31 may be the smallest number (much effort of other people is involved).
I will elaborate on this later.
What would you say, Jock? 
|
|
IP Logged |
|
|
|
JocK
Uberpuzzler
Gender:
Posts: 877
|
|
Re: packing spheres inside a cube
« Reply #5 on: Sep 2nd, 2004, 4:02pm » |
Quote Modify
|
on Sep 2nd, 2004, 5:31am, Barukh wrote:I have some evidence that N=31 may be the smallest number (much effort of other people is involved).
I will elaborate on this later.
What would you say, Jock? |
|
Nice... 
And yes, a cubic close packing of 32 unit diameter spheres fits inside a cube of volume (1+3/[sqrt]2)[sup3] [approx] 30.41. Leave out one of the 32 spheres and you have 31 spheres inside a volume smaller than 31.
But is 31 really the smallest number? I am curious to see your proof!
J CK
|
|
IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
on Sep 2nd, 2004, 4:02pm, JocK wrote:| And yes, a cubic close packing of 32 unit diameter spheres fits inside a cube of volume (1+3/[sqrt]2)[sup3] [approx] 30.41. Leave out one of the 32 spheres and you have 31 spheres inside a volume smaller than 31. |
|
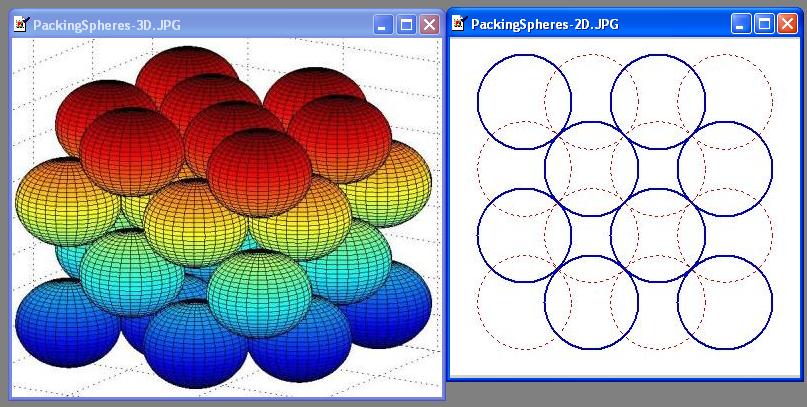
Hmm… I’ve got the same results, but I doubt it’s the cubic close packing that solves the case. See the attached drawings. In this configuration, spheres are organized in 4 layers, and each layer has a square packing (in 2-D case only two adjacent layers are shown). Every sphere touches at most 8 other spheres, whereas in CCP it is surrounded by 12 spheres.
This configuration was built from the points of sphere centers kindly sent to me by Dave Boll (He’s got a nice optimal packing site, which inspired me to think N=31 is the smallest number). It took me a while to reveal from the points the pattern of the whole configuration.
Quote:| But is 31 really the smallest number? I am curious to see your proof! |
|
I don’t have a proof in its strict sense. I doubt anybody has it today. Rather, there is an ongoing effort to improve the best known packings, using mainly computational methods. As far as I know, the optimality is proved only for N = 2-6, 8-10. The following paper contains probably the latest results in optimal sphere packing to date. Note that for N=31 it gives the same attached configuration (figure 5). The difficulty of improving the existing packings supports my opinion that N=31 is the smallest number.
It was a great pleasure to work on this problem, Jock!
P.S. After investigating the configuration closely, I realized that my claim about surrounding spheres is not correct: the spheres in the central layers do have 12 neighbors... So, maybe it is indeed a CCP?!
|
| « Last Edit: Sep 3rd, 2004, 5:15am by Barukh » |
IP Logged |
|
|
|
JocK
Uberpuzzler
Gender:
Posts: 877
|
|
Re: packing spheres inside a cube
« Reply #7 on: Sep 3rd, 2004, 2:42pm » |
Quote Modify
|
Barukh, you are perfectly right! Indeed it seems all computer simulations so far indicate that for the 3-D problem N=31 is the minimum.
I didn't know this myself, but based on your last post I decided to post the problem on the sci.math newsgroup. (In fact, whilst I had worked out the N=31 solution, I just couldn't believe it yielded indeed the minimum.) Hugo Pfoertner directed me to the following integer sequences:
http://www.research.att.com/cgi-bin/access.cgi/as/njas/sequences/eisA.cg i?Anum=A084616
(2-D case) and:
http://www.research.att.com/cgi-bin/access.cgi/as/njas/sequences/eisA.cg i?Anum=A084826
(3-D case).
These contain the solutions (computer simulation results) to both the 2-D (N=30) and the 3-D (N=31) problem. For the 3-D case, I find it very remarkable that whilst N=14 comes so close to satisfying the constraint V<N (14 unit-diameter spheres fit inside a cube of volume 14.071), this constraint is not satisfied until one reaches N=31. Moreover, for N=31 the constraint is satisfied in what seems to be a truly inefficient way (removing one sphere from a configuration of 32 spheres packed inside a cube).
However, it is difficult to argue against these computer results... (Although - as you indicated - they render it very unlikely, they don't exclude the possibility that a lower N-value can be found!)
Thanks for working this out in so much detail Barukh, I have learned a lot from it myself.
Btw: no reasons for doubt, the 3-D solution constitutes a cubic close packing!
JCK
|
| « Last Edit: Sep 3rd, 2004, 4:30pm by JocK » |
IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print