Author |
Topic: Finding the subject of the equation (Read 661 times) |
|
mattian
Senior Riddler
 
Gender: 
Posts: 404
|
 |
Finding the subject of the equation
« on: Jul 19th, 2004, 8:09am » |
 Quote  Modify
|
Given an equation
f(a) = 1 - f(a, b)
How would one make a the subject of the equation such that a is given as a function of b?
a = f(b)
For example:
Express y in terms of x such that y = f(x)
log y = 1 - 2xy
The inverse is easy - i.e.
x = f(y) = (1 - (log y)) / 2y
But simplifying and making y the subject of the equation - not so easy.
|
| « Last Edit: Jul 19th, 2004, 8:38am by mattian » |
 IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Finding the subject of the equation
« Reply #1 on: Jul 19th, 2004, 8:17am » |
Quote Modify
|
Alternatively, what techniques could be used to find y, given x?
|
| « Last Edit: Jul 19th, 2004, 8:42am by mattian » |
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Finding the subject of the equation
« Reply #2 on: Jul 19th, 2004, 2:14pm » |
Quote Modify
|
I don't think there is a general way to find either a as a function of b, nor b as a function of a, since it might not be a function in the first place..
And for instance you could have
log(y) = 1 - (2 xy + log(x) )
Which is equal to log(x) = 1 - (2 xy + log(y) ), so you have the same problem for x and y
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Finding the subject of the equation
« Reply #3 on: Jul 19th, 2004, 5:03pm » |
Quote Modify
|
So what does one do in such a situation? Successive approximations? Newton's Method, perhaps? How would one find a, given b - in a way that can be expressed mathematically?
|
|
IP Logged |
|
|
|
Jack Huizenga
Guest
|
|
Re: Finding the subject of the equation
« Reply #4 on: Jul 19th, 2004, 6:52pm » |
Quote Modify
 Remove
|
Another good example of the question you are asking is provided by the gamma function, which is an extension of the factorial function to the real line. If you want to invert the expression x=gamma(y), you don't  . The gamma function is not 1-1, and therefore there is no "inverse gamma" function. Often times in this type of situation a numerical approximation is the best you can do. Also, the correct way of dealing with such a problem is often determined by the context of the question. Recently I was proving a theorem where the conclusion was that "if r>m!, then f(r)>m". The most desirable format for the final theorem would have been something more like "f(r)>g(r)" for some function g. However, as there is no nice way to invert the factorial, stating the theorem as such would have required a loss of information. Hence, in this case, the best thing to do is just to leave the solution in the slightly less desirable but much more exact formulation. There are other situations where a particular numerical answer is more desired. However, keep in mind that something such as Newton's method will only provide a single value for a upon fixing b; it will never yield an actual function for a in terms of b.
Sadly, the vast majority of mathematical expressions cannot be inverted. We just have to deal with it .
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Finding the subject of the equation
« Reply #5 on: Jul 19th, 2004, 7:14pm » |
Quote Modify
|
Quote:| However, keep in mind that something such as Newton's method will only provide a single value for a upon fixing b; |
|
Yes - I know - I thought I might have to resort to the synthetic solution rather than rigidly hang on to the analytical one.
Well how about I post the actual problem and see how I could best represent (or solve for) y in terms of x.
Here is the equation:
sin (y/4) = 1 - x(2[pi] - y/2)
What is the best way to find y?
|
|
IP Logged |
|
|
|
Leo Broukhis
Senior Riddler
Gender:
Posts: 459
|
|
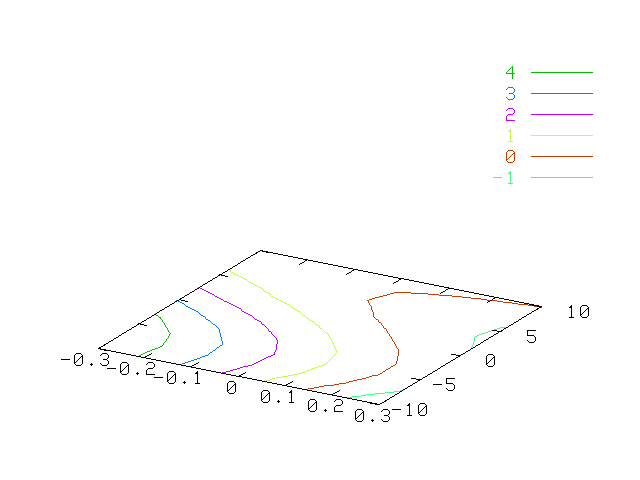
Re: Finding the subject of the equation  graph.png
« Reply #6 on: Jul 19th, 2004, 8:15pm » |
Quote Modify
|
According to gnuplot, y is not a function of x:
splot [-0.3:0.3][-10:10] 1-x*(2*pi-y/2)-sin(y/4),0
X axis is the closer one. Observe the contour line corresponding to 0.
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Finding the subject of the equation
« Reply #7 on: Jul 20th, 2004, 6:00am » |
Quote Modify
|
Hi Leonid -
Welcome to my maths question .
Regarding your graph - that's pretty much what I've done so far - and it works well. I guess I'm just one of those people who likes things (like maths expressions) to look pretty.
Thanks.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print