Author |
Topic: Geometry Problem (Read 844 times) |
|
mattian
Senior Riddler
 
Gender: 
Posts: 404
|
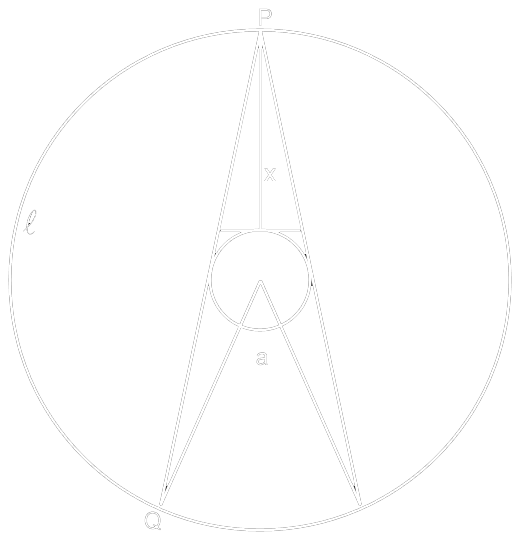
Express angle a in terms of distance x and arc length [smiley=l.gif].
Arc length [smiley=l.gif] is the shorter distance between points P and Q on the circumference of the larger circle in the diagram (see Addendum)
All visibly apparent tangents, right-angles, etc. may be assumed to be as they appear.
Addendum:
The segment [smiley=l.gif] has not been included in this diagram. Nor have points P or Q. A corrected diagram has been posted further down in this thread - please refer to the second diagram.
|
| « Last Edit: Jul 16th, 2004, 9:26pm by mattian » |
 IP Logged |
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
 |
Re: Geometry Problem
« Reply #1 on: Jul 16th, 2004, 4:22pm » |
 Quote  Modify
|
We need more infornation, so I will assume that the large circle has a unit radius. I get a=4cos-1(sqrt[x(2-x)]) for (2-sqrt(2))/2<=x<=1. I'll explain how I got it if you will allow my assumption.
By the way, mattlan, your avatar is not visible to us, as it has a reference to your local machine; you can upload your avatar when you're editing your profile, or just set the reference to a public URI.
|
|
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
Sorry about that Sir Col - I know, I realised shortly after posting it that I forgot to include one of the given quantities. Here is the correct diagram and the problem is as follows:
Express angle a in terms of distance x and arc length [smiley=l.gif]. Make all the same assumptions stated in the former submission of this problem.
Arc length [smiley=l.gif] is the shorter distance between points P and Q on the circumference of the larger circle in the diagram.
|
| « Last Edit: Jul 16th, 2004, 6:46pm by mattian » |
IP Logged |
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
|
Re: Geometry Problem
« Reply #3 on: Jul 18th, 2004, 1:02pm » |
Quote Modify
|
I'm not having much success with this; I can't obtain an explicit form.
So far...
Let the point where PQ meets the inner circle be S and the centre be O.
Let radius of inner circle be r and outer circle be R.
Using Pythagorean Theorem, (r+x)2=r2+PS2, giving 2rx+x2=PS2.
Angle at cente is a, angle at circumference is a/2, so angle QPO is a/4, and PS=Rcos(a/4).
Because r=R-x, 2rx+x2=x(2(R-x)+x)=x(2R-x)=R2cos2(a/4).
Arc length, l=(R(2[pi]-a))/2, so R=(2l)/(2[pi]-a).
This leads to the not so pleasant formula, x(2[pi]-a)(4l-(2[pi]-a)x)=4l2cos2(a/4). However, good luck to anyone who can derive angle a explicitly in terms of l and x from this! 
|
| « Last Edit: Jul 18th, 2004, 4:26pm by Sir Col » |
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Geometry Problem
« Reply #4 on: Jul 19th, 2004, 8:26am » |
Quote Modify
|
There is a simpler form for the partial solution you have so far.
I agree that
R = 2l / (2[pi] - a)
And the rest of your deductions are accurate - I think - but I think they're overly complex.
There are two stages to this problem. The first is establishing an equation which relates a, l and x. The second is separating these parameters into the form a = f(l, x). The first part is fairly straight forward and quite simple; the second part is less trivial.
|
| « Last Edit: Jul 19th, 2004, 8:36am by mattian » |
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Geometry Problem
« Reply #5 on: Jul 20th, 2004, 5:15pm » |
Quote Modify
|
My solution:
::
sin (a/4) = 1 - (x/l) * ([pi] - a/2)
::
|
|
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Geometry Problem
« Reply #6 on: Jul 21st, 2004, 4:09am » |
Quote Modify
|
Oh. I was looking for something like a = f(x,l).
|
|
IP Logged |
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
|
Re: Geometry Problem
« Reply #7 on: Jul 21st, 2004, 5:01am » |
Quote Modify
|
on Jul 20th, 2004, 5:15pm, mattian wrote:My solution:
::sin (a/4) = 1 - (x/l) * ([pi] - a/2):: |
|
I think you made a slight error, missing a 2 from the denominator...
R = r+x = Rsin(a/4)+x, so R(1-sin(a/4)) = x, and 1-sin(a/4) = x/R.
Substituting R = (2l)/(2[pi]-a), we get 1-sin(a/4) = x(2[pi]-a)/(2l), or sin(a/4) = 1-x(2[pi]-a)/(2l).
But like Grimbal, I dismissed this because you cannot rearrange it to get 'a' explicitly in terms of l and x.
Consider the even simpler equation, y = x - sin(x). Try and rearrange it to get x in terms of y. Part of the problem is that sine is periodic, so a true inverse cannot exist; however, as we have the restriction 0 [le] a [le] [pi], I wonder if anything clever can be done?
|
|
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Geometry Problem
« Reply #8 on: Jul 21st, 2004, 5:38am » |
Quote Modify
|
The two (Mattian's and Sir Col's) solutions look the same to me 
|
| « Last Edit: Jul 21st, 2004, 5:40am by Grimbal » |
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Geometry Problem
« Reply #9 on: Jul 21st, 2004, 5:51am » |
Quote Modify
|
I join Grimbal and Sir Col in what “expressing a variable in terms of other variables” means. For me, it’s deriving a direct function for it. What mattian did, is called an indirect function. It is not so easy to calculate the unknown value out of it.
on Jul 21st, 2004, 5:01am, Sir Col wrote:| Consider the even simpler equation, y = x - sin(x). Try and rearrange it to get x in terms of y. Part of the problem is that sine is periodic, so a true inverse cannot exist; however, as we have the restriction 0 [le] a [le] [pi], I wonder if anything clever can be done? |
|
Good question… You are actually asking to find the inverse of the function f(x) = x – sin(x). It is interesting how little useful information may be found on this on the Web… In a sense, it is just a matter of what is defined to be a simple function. Why do we say that f(x) = x2 has a simple inversion (namely, a square root)? Do you know that taking a square root is sometimes done using Newton-Rafson method (e.g. AMD processor does exactly that)?
Going to the edge, I may suggest SirCol(x) as an inverse to x – sin(x), or mattian(x, l) as a direct function for a.
What is also interesting: I noticed the traces of mattian’s solution on at least 2 other (apparently un-related) threads: here (reply #33), and here (reply #5).
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Geometry Problem
« Reply #10 on: Jul 21st, 2004, 6:24am » |
Quote Modify
|
Barukh,
Very observant. The Prisoner thread is the complete problem; the Geometry Problem is part of the Prisoner problem; and the Subject of the Equation problem is part of the Geometry problem.
I thought the individual components of these problems were interesting problems unto themselves so I posted them as separate threads.
Quote:| Oh. I was looking for something like a = f(x,l). |
|
I wish - check out my other thread in putnam - Finding the subject of the equation. I was originally looking for a as the subject of the equation - and would love to be able to express it that way, but I don't think that's going to happen. Sorry for the misunderstanding.
I ended up using successive approximations to resolve a result between 0 and [pi] that satisfied the equation, and the results have proved accurate so far.
Quote:| I think you made a slight error, missing a 2 from the denominator... |
|
Let R be the radius of the large circle
Let r be the radius of the small circle
then:
sin (a/4) = (r/R)
R = 2l/(2[pi] - a)
r = R - x
.: r = (2l/(2[pi] - a)) - x
.: sin (a/4) = ((2l/(2[pi] - a)) - x) / 2l/(2[pi] - a)
simplify:
let y = (2[pi] - a)
then
sin (a/4) = ((2l/y) - x) / (2l/y)
.: sin(a/4) = 1 - (x/(2l/y))
.: sin(a/4) = 1 - (xy/2l)
.: sin(a/4) = 1 - (x/l)(y/2)
substitute back:
sin(a/4) = 1 - ((x/l)(2[pi] - a)/2)
.: sin(a/4) = 1 - (x/l)([pi] - a/2)
|
| « Last Edit: Jul 21st, 2004, 6:42am by mattian » |
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Geometry Problem
« Reply #11 on: Jul 21st, 2004, 6:27am » |
Quote Modify
|
Quote:| The two (Mattian's and Sir Col's) solutions look the same to me |
|
Yup - they're the same. Just thought I would include my working too. For completeness.
|
|
IP Logged |
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
|
Re: Geometry Problem
« Reply #12 on: Jul 21st, 2004, 7:01am » |
Quote Modify
|
You're absolutely right, mattian (and Grimbal); inexcusably I missed the fact that you had divided the numerator: 2[pi]-a, by 2. Sorry! 
Picking up on Barukh's suggestion: although it is not possible to rearrange to get 'a' explicitly, we can derive an efficient iterative formula using the Newton-Raphson method.
From sin(a/4)=1-x(2[pi]-a)/(2l), write sin(a/4)+x(2[pi]-a)/(2l)-1=0.
Let f(a)=sin(a/4)+x(2[pi]-a)/(2l)-1, f'(a)=(a/4)cos(a/4)-ax/(2l).
Then we can use an+1 = an-f(an)/f'(an) to converge on a solution.
|
|
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Geometry Problem
« Reply #13 on: Jul 21st, 2004, 7:31am » |
Quote Modify
|
And now this thread is truly converging on the other one ("Finding the subject of the equation").
It does bother me though - despite the fact that I do see the elegance in convergence - that our mathematical constructs do not cater for situations such as these - where the the rules we have defined are not flexible enough to allow us to express things cleanly.
We know for example, that the plot of a against (x/l) looks like a function which could be expressed as a = f(x,l) and yet we don't have the vocabulary to express it. I see it in the same light as complex numbers (except that we have established ways of dealing with those), in that our original set of mathematical rules were written without the foresight (understandably so) to accommodate the mathematical discoveries that would follow.
Which brings me to the following idea. Would it not be more interesting to converge on a function that describes a in terms of (x/l) rather than converging on a for a particular (x/l). Perhaps by treating a(x,l) as a signal which we approximate with a fourier series. Given the sinusoidal characteristics in a, I doubt it would resolve to a very complex expression. Two or three terms should probably suffice in the range 0 to [pi].
|
| « Last Edit: Jul 21st, 2004, 7:32am by mattian » |
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print