Author |
Topic: Rectangles with one integer dimension (Read 2270 times) |
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender: 
Posts: 7527
|
 |
Rectangles with one integer dimension
« on: Jun 21st, 2004, 1:47pm » |
 Quote  Modify
|
Here is a problem I saw on a forum, but without a solution. For time being, I have been unable to prove or disprove it.
Suppose you have a rectangle that is subdivided into a finite number of smaller rectangles of various sizes, completely filling the rectangle and with no overlap. Suppose that each of the small rectangles has the property that one of its dimension is an integer. Prove that the outer rectangle also has this property.
|
|
 IP Logged |
|
|
|
TenaliRaman
Uberpuzzler
I am no special. I am only passionately curious.
Gender:
Posts: 1001
|
|
Re: Rectangles with one integer dimension
« Reply #1 on: Jun 21st, 2004, 3:33pm » |
Quote Modify
|
::
if i have not mistaken the question,
i assume that if a rectangle has 1 integer dimension that means there is a pair of opposite sides with integer length.
in which case,
i think the proof is easy.
we know that,
p->q is equivalent to ~q->~p
p : all smaller rectangles have integer dimensions
q : bigger rectangle has integer dimension
we will show ~q->~p
i.e if the bigger rectangle has no integer dimensions then all the smaller rectangles cannot have integer dimension.
Assume we have a large rectangle with no integer dimension.
Now since we have to divide it into rectangles, we can either have a horizontal cut or vertical cut.
Can i divide this rectangle into two rectangles having one integer dimension? No, one of them will have no integer dimensions.
Following this argument recursively, we see that there will be atleast one rectangle which does not have integer dimension.
::
|
|
IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Rectangles with one integer dimension
« Reply #2 on: Jun 22nd, 2004, 12:54am » |
Quote Modify
|
But aren't you assuming each cut goes through a whole (sub)rectangle?
You could never get something like
[][][]
[][][]
[][][]
So it doesn't apply to all possible divisions of a rectangle, only ones were you make whole cuts recursively
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Rectangles with one integer dimension
« Reply #3 on: Jun 23rd, 2004, 1:25am » |
Quote Modify
|
This statement is indeed true. Here’s a sketch of increadibly simple proof due to Solomon Golomb, the inventor of polyominos.
[smiley=blacksquare.gif]
The proof is by contradiction. Assume that both dimensions of the outer rectangle are not integers.
Imagine an infinite chess-board drawn on the plane, with the side length equal to 1/2. Put the outer rectangle on the plane so that its left and bottom sides are lined up with the lines of the chess-board. Now there are two crusial facts (Try to prove them):
1. Because of the assumption made, the outer rectangle will cover non-equal area of black and white color.
2. Because every small rectangle has at least one integral side, it will cover the same area of black and white color.
That’s the contradiction.
[smiley=blacksquare.gif]
IMHO, extremely elegant!
|
|
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Rectangles with one integer dimension
« Reply #4 on: Jun 23rd, 2004, 11:53am » |
Quote Modify
|
Wow! Elegant indeed.
|
|
IP Logged |
|
|
|
TenaliRaman
Uberpuzzler
I am no special. I am only passionately curious.
Gender:
Posts: 1001
|
|
Re: Rectangles with one integer dimension
« Reply #5 on: Jun 25th, 2004, 10:49am » |
Quote Modify
|
Yes you are right towr! I almost convinced myself that any form of cuts can be simulated with a recursive sequence of cuts.Ofcourse ur simple example counters everything i had in mind!
Barukh,
that is really cool!
I am trying to prove the two facts.Unfortunately, these "facts" are not very intuitive (IMHO). Which basically means i have no clue as to how to start proving them. Anyways will try and see if i can get around it. 
|
|
IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
TenaliRaman
Uberpuzzler
I am no special. I am only passionately curious.
Gender:
Posts: 1001
|
|
Re: Rectangles with one integer dimension
« Reply #6 on: Jul 2nd, 2004, 2:27pm » |
Quote Modify
|
Not able to convince myself of the two facts yet. Any help is greatly appreciated!!
|
|
IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Rectangles with one integer dimension
« Reply #7 on: Jul 3rd, 2004, 4:29am » |
Quote Modify
|
on Jul 2nd, 2004, 2:27pm, TenaliRaman wrote:| Not able to convince myself of the two facts yet. Any help is greatly appreciated!! |
|
Here's a hint for fact #2: What happens if the small rectangle is moved in the direction perpendicular to its integral side?
Hope this helps...
|
|
IP Logged |
|
|
|
TenaliRaman
Uberpuzzler
I am no special. I am only passionately curious.
Gender:
Posts: 1001
|
|
Re: Rectangles with one integer dimension
« Reply #8 on: Jul 8th, 2004, 9:19am » |
Quote Modify
|
i need a new brain
i am not seeing anything yet! 
|
|
IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Rectangles with one integer dimension
« Reply #9 on: Jul 8th, 2004, 10:14am » |
Quote Modify
|
You could try drawing it..
Also, integer length line pieces parallel to any of the sides must be collored equally much black as white, so the same goes for a rectangle with an integer side (just cut it up into lines)
|
| « Last Edit: Jul 8th, 2004, 10:43am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
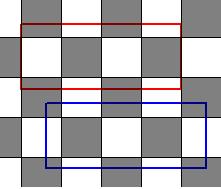
TenaliRaman, look at the attached drawing. The blue is the originial position of the rectangle, the red is where it was moved to coincide with the chessboard lines at its integer side.
|
|
IP Logged |
|
|
|
TenaliRaman
Uberpuzzler
I am no special. I am only passionately curious.
Gender:
Posts: 1001
|
|
Re: Rectangles with one integer dimension
« Reply #11 on: Jul 10th, 2004, 10:41am » |
Quote Modify
|
duh! its so embarassingly obvious!!!
Thanks towr and Barukh!
Its ofcourse trivial now as to why Mr Solomon chose the sides to be 1/2, it offers such a simple proof for the first fact!!!
(Simply Brilliant i would say brilliant!!)
|
|
IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Rectangles with one integer dimension
« Reply #12 on: Jul 13th, 2004, 9:20am » |
Quote Modify
|
You may want to look at the following paper for more proofs, generalizations and references.
The complex integration method is amazing! 
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print