Author |
Topic: Square Folding Curiosity (Read 645 times) |
|
Perfection
Newbie
Gender: 
Posts: 17
|
 |
Square Folding Curiosity
« on: Mar 13th, 2004, 11:30pm » |
 Quote  Modify
|
So today I was just you know, chillin', hangin' out and what-not and I came up with an interesting question
If I were to take a 1x1 piece of paper (negligible depth, infinite flexibility, cannot be ripped) what is the largest distance I can get between 4 points if it is required that they all be equidistant?
So I knew it must somehow reach all vertices of a tetrahedron, and since I knew that two equilaterial triangles sharing two points meet those requirements I realized the largest one that could be made on the paper had the diagonal for altitudes and met at the other one giving me a rhombus with side lengths of sqrt(2/3). Here's the fun part, is this the true solution or is there some way to make the 4 equistant points farther out with the 1x1 square.
|
|
 IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Square Folding Curiosity
« Reply #1 on: May 27th, 2004, 6:04pm » |
Quote Modify
|
I think you can have the 4 points at the summit of a tetrahedron with side 1. It is a little difficult to explain,though.
Make the construction you did, but make the common base of the triangles with length 1. Fold 90° down along the base, fold up along the sides of the triangles and at the ends of the diagonal. You should have the 4 corners on a perfect tetrahedron.
|
|
IP Logged |
|
|
|
SWF
Uberpuzzler
Posts: 879
|
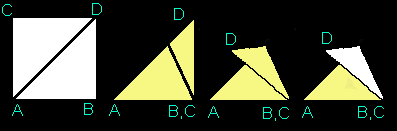
In the figure below the paper is white on one side, yellow on the other.
1) Fold along diagonal to make triange
2) Fold back and forth on black line (I did not calculate exact position- might be drawn out of proportion).
3) To get from position in third figure to that in forth figure, you need to open up the paper and flip the portion with D on in inside out.
ut of proportion).
4) Open up until distance from B to C is 1, and if the position of fold in step 2 was correct, D will be distance 1 from A, B, and C.
|
|
IP Logged |
|
|
|
Perfection
Newbie
Gender:
Posts: 17
|
|
Re: Square Folding Curiosity
« Reply #3 on: Jun 6th, 2004, 8:40pm » |
Quote Modify
|
Okay, now I'm confused.
Would it be possible for one you fine folks post an unfolded versian showing where all the fold lines are?
That would make me very happy!
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print