Author |
Topic: Ellipse Area Triangle (Read 1484 times) |
|
Benoit_Mandelbrot
Junior Member
Almost doesn't count.
Gender: 
Posts: 133
|
 |
Ellipse Area Triangle
« on: Feb 17th, 2004, 8:48am » |
 Quote  Modify
|
Find the equation of the line tangent to the ellipse:
b2*x2 + a2*y2 = a2*b2
in the first quadrant that forms with the coordinate axes the triangle of smallest possible area (a & b are positive constants).
|
|
 IP Logged |
Because of modulo, different bases, and significant digits, all numbers equal each other!
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Ellipse Area Triangle
« Reply #1 on: Feb 17th, 2004, 10:06am » |
Quote Modify
|
interesting, I get a triangle area of ::a*b::
And to answer the question, line :: y = b (sqrt(2) - x/a) ::
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
John_Gaughan
Uberpuzzler
Behold, the power of cheese!
    
Gender:
Posts: 767
|
|
Re: Ellipse Area Triangle
« Reply #2 on: Feb 17th, 2004, 11:51am » |
Quote Modify
|
Towr, how did you arrive at your answer? Given that this is the first quadrant, I was able to simplify to :: y == (b/a) sqrt (a2 - x2), where x and y are positive and a > x. I imagine I need to take the derivative of this equation to get the slope of the line, but I don't remember offhand how to do it in this case. I am at work, my books are at home. ::
|
|
IP Logged |
x = (0x2B | ~0x2B)
x == the_question
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Ellipse Area Triangle
« Reply #3 on: Feb 17th, 2004, 12:06pm » |
Quote Modify
|
yep, that's how I started.. I have the luck of having my computer to do some of the 'hard' work, but you can just use the chain rule (I think that's what it's called) ::df(u)/dx = df(u)/du du/dx
and of course in this case f(u) = (b/a) sqrt(u), and u = (a2 - x2) ::
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
John_Gaughan
Uberpuzzler
Behold, the power of cheese!
Gender:
Posts: 767
|
I screwed something up I think... attached is the line I wound up with. It is in y=mx+b format.
|
|
IP Logged |
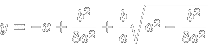
x = (0x2B | ~0x2B)
x == the_question
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Ellipse Area Triangle
« Reply #5 on: Feb 17th, 2004, 1:51pm » |
Quote Modify
|
::
starting at y = f(x) = (b/a) sqrt (a2 - x2),
the tangent line to the ellips at a point on the upper arc has direction
f'(x) = (b/a) * 1/2 / sqrt (a2 - x2) * (-2x)
= -x (b/a) / sqrt (a2 - x2)
the line we're looking for will cross through some point (x,y)min, where the triangle is minimized
so we have
y - ymin = f'(xmin)(x-xmin)
y = f(xmin) + f'(xmin)(x-xmin )
y = b (a2 - xminx)/(a sqrt(a2 - xmin2))
from this line we'll need y when x=0, and x when y=0 (the points where the line crosses the axis)
so y = ab/( sqrt(a2 - xmin2))
and 0 = b (a2 - xminx)/(a sqrt(a2 - xmin2))
=> x = a2/xmin
the size of the triangle (x*y/2) is minimized when we minimize
x*y = a3b/(xminsqrt(a2 - xmin2))
To do this we'll finally determine xmin, so take the derivative and find where it is 0; eventually we get xmin = sqrt(2)a/2 (among other solutions which don't fit our needs)
So filling this in in our description of the line, y = b (a2 - xminx)/(a sqrt(a2 - xmin2))
we get y = b(sqrt(2) a - x)/a
::
|
| « Last Edit: Feb 17th, 2004, 1:56pm by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print