Author |
Topic: Tangential N-Spheres (Read 4844 times) |
|
Barukh
Uberpuzzler
Gender: 
Posts: 2276
|
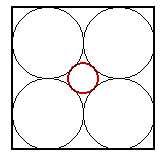
Consider the square with the unit side length and four inscribed circles tangent in pairs (see the attached drawing). The fifth (red) circle is tangent to these four.
Analogiously, we may construct the configuration in 3-dimensional space in the unit cube and get the tangential sphere in the center.
The problem is to investigate the size and volume of the tangential N-sphere in N-dimensional space.
|
| « Last Edit: Oct 4th, 2003, 11:48am by Barukh » |
 IP Logged |
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
 |
Re: Tangential N-Spheres
« Reply #1 on: Oct 4th, 2003, 1:43pm » |
 Quote  Modify
|
My understanding of geometry is limited to 3-d space, but I'll have a go...
::
In 2- and 3-dimensional space, the distance from the centre of the large circle/sphere (radius R) to the centre of the small circle/sphere (radius r), is R+r.
On a 2-d plane, we can split the unit square into four smaller squares.
In 3-d space, we can split the unit cube into eight smaller cubes.
The large circle/sphere is centred in the centre of each newly created square/cube.
The small circle/sphere is centred in the centre of the unit square/cube.
Using the Pythagorean theorem...
2-d: (R+r)2=R2+R2=2R2, so r=[pm]R([sqrt]2–1).
3-d: (R+r)2=R2+R2+R2=3R2, so r=[pm]R([sqrt]3–1).
In both cases, R=1/4.
Leading to a generalisation for N space, r=[pm]R([sqrt]N–1)?
::
I've probably made a hideous error, as I don't know how geometry applies to higher dimensions.
|
|
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Tangential N-Spheres
« Reply #2 on: Oct 4th, 2003, 7:45pm » |
Quote Modify
|
Fill around your hypercube with identical cubes, and place more of the smaller hyperspheres in every interstitial location. Now consider two of the smaller spheres which are diametrically opposed across one of the larger spheres. Because 2 of the larger spheres fill the unit cube in each direction, their diameters are 1/2. Thus the distances in the principle directions between the centers of the two smaller spheres is also 1/2. Applying the n-dimensional version of the Pythagorean theorem tells you that the direct distance between the two centers is ((1/2)2 + (1/2)2 + ... + (1/2)2)1/2 = ([sqrt]n)/2. But this distance is the sum of the diameter of the small sphere + the diameter of the large sphere. Thus the smaller sphere has diameter ([sqrt]n)/2 - 1/2. And the radius is
([sqrt]n - 1)/4.
To investigate the volume would require that I look up or rederive the n-volume formula for an n-dimensional hypersphere - which is fairly nasty, picking up another power of [pi] with every even dimension.
|
| « Last Edit: Oct 4th, 2003, 8:00pm by Icarus » |
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Tangential N-Spheres
« Reply #3 on: Oct 5th, 2003, 7:21am » |
Quote Modify
|
Sir Col and Icarus, you are both right. I had no doubt the calculation of the radius won't take too much time. The reason I proposed this problem, is to drive your attention to the following:
The result is counter-intuitive (at least for me): The configuration suggests the N-sphere is "inside" the N-cube. However, its radius tend to infinity, whereas the side of the cube is 1.
What is even more striking (if my calculations are correct), is the fact that also the volume of this sphere tends to infinity! Maybe, somebody of you will take his time to assure or disprove this result. Here's the link with all the needed information: http://mathworld.wolfram.com/Hypersphere.html, formulas (4), (9).
Strange and beatifull at the same time!
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Tangential N-Spheres
« Reply #4 on: Oct 5th, 2003, 11:11am » |
Quote Modify
|
I haven't had time to sort out the formula yet, but something must be wrong. The n-volume of the unit hypercube is 1. This sphere is contained inside the hypercube. By the definition of n-volume, the sphere's volume must be smaller than the hypercube's.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
|
Re: Tangential N-Spheres
« Reply #5 on: Oct 5th, 2003, 12:34pm » |
Quote Modify
|
For the N-sphere to be contained inside the N-cube, r[le]1/2. Solving this, we get ([sqrt]N–1)/4[le]1/2, giving N[le]3. In other words, is it suggesting that for the N-sphere to be contained, we are restricted to 3-dimensions, and a tangential sphere in higher dimensions will extend beyond the N-cube?
|
|
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Tangential N-Spheres
« Reply #6 on: Oct 5th, 2003, 1:02pm » |
Quote Modify
|
Yes I see, except that you dropped the square root. It is [sqrt]N [le] 3, so N [le] 9.
This makes matters slightly easier to swallow for me. It seems incredible that the switch to 4 dimensions would so change matters as to allow this to happen, but 10 dimensions is so far beyond our 2 & 3 dimensional vision that it is less implausible.
It is curious enough that in 4 dimensions that "little" gap filling sphere is just as big as the others
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
|
Re: Tangential N-Spheres
« Reply #7 on: Oct 5th, 2003, 1:43pm » |
Quote Modify
|
Oops, good spot, Icarus! That is strange about the 4-dimensional sphere; higher dimensions are so weird. Could someone please draw me a picture so I can see what's going on? 
|
|
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Tangential N-Spheres
« Reply #8 on: Oct 6th, 2003, 11:47am » |
Quote Modify
|
on Oct 5th, 2003, 11:11am, Icarus wrote:| I haven't had time to sort out the formula yet, but something must be wrong. The n-volume of the unit hypercube is 1. This sphere is contained inside the hypercube. By the definition of n-volume, the sphere's volume must be smaller than the hypercube's. |
|
Ah, I think that's a good example of how our intuition deceives us! Here's the derivation, and try to disprove it:
Consider the case N=2k. Then, the volume V=R2k[pi]k/k! ~ (2k[pi])k/k!42k for big k. Using Stirling approximation for k!, we arrive at the following formula:
V ~ ( [pi]e/8 )k/(2[pi]k)1/2
But [pi]e is (slightly) bigger than 8, so V goes to infinity.
on Oct 5th, 2003, 1:43pm, Sir Col wrote:| higher dimensions are so weird. Could someone please draw me a picture so I can see what's going on? |
|
I can't imagine them too. The best thing is to rely on exact definitions and perform correct calculations...
Maybe, the following link will be of some help:
http://www.mathreference.com/ca-int,hsp.html
http://www.megafoundation.org/UltraHIQ/HIQNews/Hypersphere.doc
|
|
IP Logged |
|
|
|
James Fingas
Uberpuzzler
Gender:
Posts: 949
|
on Oct 5th, 2003, 1:43pm, Sir Col wrote:| Could someone please draw me a picture so I can see what's going on? |
|
Here's my best shot at a picture. I'm drawing a two-dimensional grid of two-dimensional slices. You can see that every additional dimension adds more space in the middle for the center sphere (coloured red). I'm sure my drawing's not to scale, but hopefully it'll be clear anyways. The tangency point will be somewhere along the line from one sphere's center to another sphere's center. Near the center of the tangential hypersphere, there are no constraints at all on its size.
|
|
IP Logged |
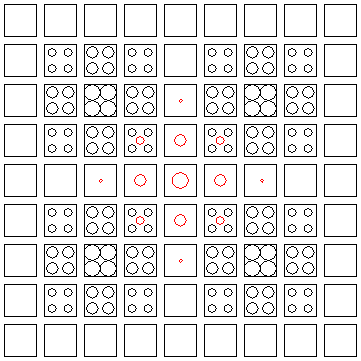
Doc, I'm addicted to advice! What should I do?
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Tangential N-Spheres
« Reply #10 on: Oct 6th, 2003, 7:30pm » |
Quote Modify
|
Of course my failing was the belief that the inner sphere would always be contained within the hypercube. But for n > 9 this is no longer true.
Perhaps James will create a 10-dimensional set of slices so we can see? 
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: Tangential N-Spheres
« Reply #11 on: Oct 6th, 2003, 7:50pm » |
Quote Modify
|
I am not sure why this result would be considerd counterintuitive. The distance from the center to a corner of the cube increases with N, but the diameter of the corner spheres does not change. Even in two-dimensions, circles in the corners of a square which are much smaller than the square's diagonal result in a central tangent circle that goes beyond the edges of the square.
The 2N spheres in the corners of the N-cube are very loosely packed, and for spheres contained by the cube, are spread as far away as possible from the center of the cube. Each of the 2N spheres only touches N of the others. With increasing N, the fraction of the cube's volume occupied by the corner spheres gets progressively smaller leaving more room at the center for a larger tangent sphere.
I would find it very counterintuitive if the interstitial sites in a densely packed arrangment resulted in a tangent sphere larger than the densely packed spheres. Of course, if that occurred the original arrangement could not have been very dense...
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Tangential N-Spheres
« Reply #12 on: Oct 7th, 2003, 12:18pm » |
Quote Modify
|
on Oct 6th, 2003, 7:50pm, SWF wrote:| The 2N spheres in the corners of the N-cube are very loosely packed, and for spheres contained by the cube, are spread as far away as possible from the center of the cube. Each of the 2N spheres only touches N of the others. With increasing N, the fraction of the cube's volume occupied by the corner spheres gets progressively smaller leaving more room at the center for a larger tangent sphere. |
|
SWF, your considerations are interesting, but as they go, it seems that the volume of the tangential hypersphere can only reach the volume of the hypercube, which is not the case: the latter is always 1, while the former grows unboundedly!
Isn't it counter-intuitive?! 
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Tangential N-Spheres
« Reply #13 on: Oct 7th, 2003, 12:20pm » |
Quote Modify
|
on Oct 6th, 2003, 1:51pm, James Fingas wrote:| Here's my best shot at a picture. |
|
James, thanks for the nice pictures. Could you please elaborate on them as I am not sure I understood them?
It becomes a tradition for me to ask you for some explanation...
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Tangential N-Spheres
« Reply #14 on: Oct 7th, 2003, 12:48pm » |
Quote Modify
|
To show something 4 dimensional in two dimensions, you have to spread out the other two dimensions (taking slices at certain intervals f.i.). In this case he did it horizontally and vertically.
If we had animation and stereoscopy it could be done in time and space..
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
James Fingas
Uberpuzzler
Gender:
Posts: 949
|
|
Re: Tangential N-Spheres
« Reply #15 on: Oct 7th, 2003, 12:49pm » |
Quote Modify
|
All right, I'll try for an explanation, but it's anyone's guess as to whether or not it will be helpful.
To start, the diagram doesn't show the whole four dimensions. It shows two dimensions completely, and then shows slices in the other two dimensions. It would be as if I took a three-dimensional object, sliced it with a series of parallel planes, and then layed out the slices in order. If you take the third column from the left of my diagram and assemble it, it should look like the three-dimensional version of this problem.
What I've done in this case is a little different. I sliced it first in the fourth dimension to produce three-dimensional slices, then sliced it in the third dimension to produce two-dimensional slices (because two-dimensional things are easier to draw!). Each square is a single two-dimensional slice, corresponding to fixing the third and fourth dimension coordinates.
The red circles that I draw show the tangential 4-sphere that is located in the center of the 4-hypercube. Right in the center, the sphere is largest, and it gets smaller in every direction.
If it helps, you could picture the fourth dimension as time, and look at every column as 2D slices of a three-dimensional object. Then reading the columns in order shows the time progression of this three dimensional object. The tangency constraint then says that at some specific times, the red sphere is tangent to all sixteen black spheres.
Now I'm at a loss because I don't know what else to explain. Maybe if you have any more specific questions, I can try to answer them or demonstrate what this would mean in 3D.
|
| « Last Edit: Oct 7th, 2003, 12:50pm by James Fingas » |
IP Logged |
Doc, I'm addicted to advice! What should I do?
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: Tangential N-Spheres
« Reply #16 on: Oct 7th, 2003, 7:50pm » |
Quote Modify
|
on Oct 7th, 2003, 12:18pm, Barukh wrote:
it seems that the volume of the tangential hypersphere can only reach the volume of the hypercube, which is not the case: the latter is always 1, while the former grows unboundedly!
Isn't it counter-intuitive?!
|
|
If I really think hard about this, maybe I can come up with a reason why this should be counterintuitive. 
Seems to me, as N increases the size of the sphere approaches that of the circumscribing sphere of the N-cube. Diameter of circumscribing sphere is equal to the long diagonal of the cube, which grows to infinity as [sqrt]N.
The counterintuitive point may be that a N-cube of unit volume would have a long diagonal whose length grows as [sqrt]N.
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Tangential N-Spheres
« Reply #17 on: Oct 8th, 2003, 12:30pm » |
Quote Modify
|
on Oct 7th, 2003, 12:49pm, James Fingas wrote:| All right, I'll try for an explanation, but it's anyone's guess as to whether or not it will be helpful. |
|
James, thank you. It really helped.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print