Author |
Topic: polynomial func with positive real image (Read 1700 times) |
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: polynomial func with positive real image
« Reply #1 on: Aug 30th, 2003, 2:06pm » |
 Quote  Modify
|
By "positive real numbers" are you including 0 or not?
If you are, then x2y2 is an obvious choice.
If not, it's not possible, unless you are allowing some restriction of the domain.
|
|
 IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
|
Re: polynomial func with positive real image
« Reply #2 on: Aug 31st, 2003, 3:43am » |
Quote Modify
|
I assume the desired image does not include 0, because then the problem would be pretty easy. I don't know the answer, nor any more about the problem than the phrasing given above, which is taken verbatim from the person who gave the problem to me. He's some math guy who calls the problem "a puzzle [he] likes". Can you prove that it's not possible without domain restriction?
|
| « Last Edit: Aug 31st, 2003, 3:44am by william wu » |
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: polynomial func with positive real image
« Reply #3 on: Aug 31st, 2003, 12:48pm » |
Quote Modify
|
Yes: I assume there are other ways of seeing it, but here is how I did:
In the .999... thread I gave a very brief overview of topology. It is topological considerations that I use here. A set [smiley=ca.gif] is open in [bbr][supn] if for every point [smiley=x.gif] [in] [smiley=ca.gif], there is a ball [smiley=cb.gif][smiley=subr.gif]([smiley=x.gif]) centered on [smiley=x.gif] with radius [smiley=r.gif] > 0 which is entirely contained in [smiley=ca.gif].
Essentially, [smiley=ca.gif] is open if it contains no points on its border. A set is closed if it contains all of its border points. (A subset of [bbr] is open iff it is a collection of disjoint open intervals.)
A subset [smiley=cx.gif] of any topological space is compact if and only if every open covering of [smiley=cx.gif] (a collection {[smiley=ca.gif][subi]} of open sets with [smiley=cx.gif] [subseteq] [bigcup][smiley=ca.gif][subi]) has a finite subcover (a finite subcollection which still covers [smiley=cx.gif]).
It turns out that any subset of [bbr][supn] is compact if and only if it is both closed (i.e. its complement is open) and bounded ([exists] [smiley=cr.gif] [in] [bbr] such that every element of the set has magnitude < [smiley=cr.gif]).
An important property of compact sets is that compactness is preserved by continuous functions: if [smiley=ca.gif] [subseteq] [smiley=cx.gif] is compact, and [smiley=f.gif] : [smiley=cx.gif] [to] [smiley=cy.gif] is continuous, then [smiley=f.gif]([smiley=ca.gif]) = { [smiley=f.gif]([smiley=x.gif]) : [smiley=x.gif] [in] [smiley=ca.gif]} is a compact subset of [smiley=cy.gif].
Apply this to our situation: let [smiley=cp.gif] : [bbr][supn] [to] [bbr] be a polynomial. Polynomials are continuous, and they also have this easily proven property: For any [smiley=cn.gif] > 0, [exists] [smiley=cr.gif] such that if [smiley=x.gif] [in] [bbr][supn] and | [smiley=x.gif] | > [smiley=cr.gif], then | [smiley=cp.gif]([smiley=x.gif]) | > [smiley=cn.gif].
Assume 0 is not in the image of [smiley=cp.gif].
Let [smiley=cn.gif] = 1, and let [smiley=cr.gif] be as described. Let [smiley=cb.gif] = { [smiley=x.gif] : | [smiley=x.gif] [le] [smiley=cr.gif] } be the closed ball of radius [smiley=cr.gif] about the origin in [bbr][supn]. [smiley=cb.gif] is closed and bounded, so it is compact. Thus [smiley=cp.gif]([smiley=cb.gif]) is compact, and is thus also closed. Since 0 [notin] [smiley=cp.gif]([smiley=cb.gif]), there must be some [epsilon] > 0 such that (-[epsilon], [epsilon]) is disjoint from [smiley=cp.gif]([smiley=cb.gif]) - otherwise 0 would be a boundary point of [smiley=cp.gif]([smiley=cb.gif]) and thus contained in [smiley=cp.gif]([smiley=cb.gif]).
So if [smiley=x.gif] [in] [smiley=cb.gif], then | [smiley=cp.gif]([smiley=x.gif]) | > [epsilon], and if [smiley=x.gif] [notin] [smiley=cb.gif], then | [smiley=cp.gif]([smiley=x.gif]) | > 1. In either case, [smiley=cp.gif] is bounded away from 0, and so the image of [smiley=cp.gif] cannot be (0, [infty]). QED
By bringing in another topological concept (connectedness), I can prove that the image of any polynomial from [bbr][supn] [to] [bbr] has to be one of the following:- [bbr],
- {[smiley=b.gif]} for some [smiley=b.gif] [in] [bbr] (if the degree is 0),
- [[smiley=b.gif], [infty]) for some [smiley=b.gif] [in] [bbr], or
- (-[infty], [smiley=b.gif]] for some [smiley=b.gif] [in] [bbr].
(0, [infty]) is not in this list.
The only part of the proof that requires [smiley=cp.gif] to be a polynomial is the part that shows there is some [smiley=cr.gif] such that for all [smiley=x.gif] with | [smiley=x.gif] | > [smiley=cr.gif], [smiley=cp.gif]([smiley=x.gif]) is bounded away from 0. Any other continuous function with this property also cannot have (0, [infty]) as its image.
Also, 0 can be replaced with any other real number and the theorem and its generalizations will still hold.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
I read your post several times, but I don't get it. Sorry  Some of these terms are brand new to me.
1. How does the compactness of B imply that P(B) is compact?
2. Why does (0 is a boundary point of P(B)) imply that 0 is contained in P(B)? Consider the set A = { (1/2)k | k [in][bbn]}. Then 2 is a boundary point, because every neighborhood of 2 contains points in A and points not in A. Yet 2 is not contained in A.
edit: I meant to say 0 is a boundary point, yet 0 is not contained in A
3. What was the purpose of the line that starts: "Polynomials have this easily proven property ..."
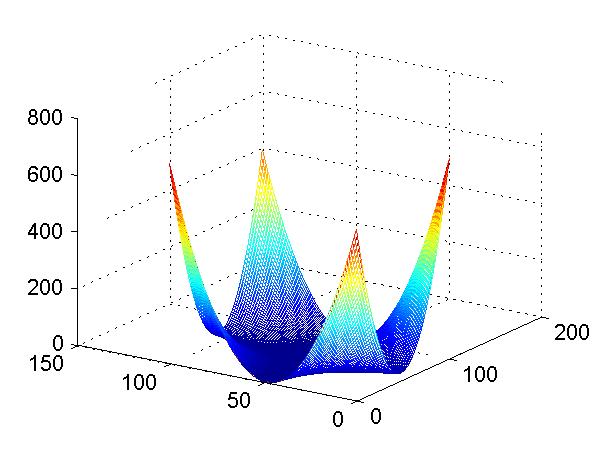
4. I think the following formula works ... is there something wrong with it?
:: (hidden) f(x,y) = (xy - 1)2 + y2 ::
:: Justification (hidden)
- f(x,y) cannot be negative since it is the sum of squares
- f(x,y) cannot be 0. Pf: Suppose f(x,y) = 0. Then
0 = (xy-1)[sup2] + y[sup2]
-y[sup2] = (xy-1)[sup2]
But the right hand side can never be negative. Contradiction.
- f(x,y) clearly hits all large positive reals, but it can also come arbitrarily close to 0 from above. Substitute y = 1/x. Then we have f(x,1/x) = 0 + (1/x)[sup2].
Graph of candidate solution shown below:
|
| « Last Edit: Sep 4th, 2003, 7:57pm by william wu » |
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: polynomial func with positive real image
« Reply #5 on: Sep 4th, 2003, 7:41pm » |
Quote Modify
|
on Sep 4th, 2003, 6:53pm, william wu wrote:| I read your post several times, but I don't get it. Sorry Some of these terms are brand new to me. |
|
Yeah, I was afraid of that. If you're not already familiar with topology, my attempts to explain it are not nearly enough to make it clear.
Quote:
1. How does the compactness of B imply that P(B) is compact?
|
|
Basic property of compactness. To prove it, you can use the "toplogical definition" of continuity: f is continuous if f[supminus][sup1](A) is open whenever A is an open set. An open cover of P(B) provides by P[supminus][sup1] an open cover of B, whose finite subcover corresponds to what must be a finite subcover of P(B).
Of course, even if you manage to figure out what I just said, it just brings the question of why the condition I gave is equivalent to f being continuous.
Unfortunately, only a systematic study of topology is going to clear up these questions. On the other hand, Topology is a very powerful theory which is relatively easy to pick up, so if you want to broaden you math education, I highly recommend it. Alas, it does not particularly apply to computer science or (at least not directly) to electrical engineering, so it may not be something you want to get into right now.
Quote:
2. Why does (0 is a boundary point of P(B)) imply that 0 is contained in P(B)? Consider the set A = { (1/2)k | k [in][bbn]}. Then 2 is a boundary point, because every neighborhood of 2 contains points in A and points not in A. Yet 2 is not contained in A. |
|
Did you mean 0, not 2? But A is not a closed set, for exactly this reason: It has a boundary point that is not part of it. P(B) must be closed, since it is compact and all compact sets are closed (another theorem). Thus any boundary points of P(B) must be inside it.
Quote:| 3. What was the purpose of the line that starts: "Polynomials have this easily proven property ..." |
|
Because of the property, I can break [bbr][sup2] up into two parts. A solid sphere, which is compact, and thus I can apply the topology to say that if P approaches 0 for points inside the sphere, then P must actually take on the value of 0.
And the exterior of the same sphere, on which (if the sphere is large enough) P is bounded away from 0 by the behaviour of polynomials.
Quote:4. I think the following formula works ... is there something wrong with it?
:: (hidden) f(x,y) = (xy - 1)2 + y2 ::
|
|
Yes - it's not nice for you to catch me in making silly hidden assumptions! 
My reply to 3 would be correct if the sentence in question was actually true. I foolishly was thinking of a property of complex (and real) polynomials of a single variable. If P(x,y) = |f(x+iy)|[sup2], where f is complex polynomial, then what I said would be true. But for general polynomials of two variables, you cannot guarantee that |P(x(s), y(s))| [to] [infty] as x[sup2] + y[sup2] [to] [infty] for an arbitrary path (x(s), y(s)). 
So obviously, I blew it. The task is possible, and your polynomial does it. Sigh!!!! There goes my claim of infallibility! 
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print