 Author
Author |
Topic: Analog clock (Read 15630 times) |
|
Nick
Guest

|
Dear all,
One more, 2nd last one...
Imagine an analog clock set to 12 o'clock. Note that the hour and minute hands overlap. How many times each day do both the hour and minute hands overlap? How would you determine the exact times of the day that this occurs?
Nick
|
|
 IP Logged IP Logged |
|
|
|
Guest
Guest

|
My wild guess would be 24 times for each hour of the day, since it overlaps once each hour. But not sure how to determine the exact time...?  .......any ideas folks... .......any ideas folks...
|
|
 IP Logged IP Logged |
|
|
|
mistysakura
Junior Member
 

Gender: 
Posts: 121
|
 |
Re: Analog clock
« Reply #2 on: May 15th, 2003, 3:10am » |
 Quote Quote  Modify Modify
|
Since it is microsoft, sit there and watch it happen. or become a program desinger for Microsoft and write a program that does specifically this, and have a normal clock as the demo.
As for the answer, I believe everyone has heard of this riddle before.
|
|
 IP Logged IP Logged |
|
|
|
Chewdog
Newbie


  
Gender: 
Posts: 50
|
 |
Re: Analog clock
« Reply #3 on: Jul 11th, 2003, 9:08am » |
 Quote Quote  Modify Modify
|
Well the hands will overlap every hour, but not on the hour. For example when it's 11:59, the hands will over lap in one minute on the 12. But When it's 12:59 you still have to wait 6 minutes before the hands overlap on the 1, becuase we cant forget that the hour hand moves too. So if you make a list, i think the times will be
12:00 am/pm
1:05 am/pm
2:10 am/pm
3:15 am/pm
4:20 am/pm
5:25 am/pm
6:30 am/pm
7:35 am/pm
8:40 am/pm
9:45 am/pm
10:50 am/pm
11:55 am/pm
That comes to a grand total of 24 times!
|
|
 IP Logged IP Logged |
|
|
|
mistysakura
Junior Member
 

Gender: 
Posts: 121
|
 |
Re: Analog clock
« Reply #4 on: Jul 11th, 2003, 10:16pm » |
 Quote Quote  Modify Modify
|
on Jul 11th, 2003, 9:08am, Chewdogscp wrote:Well the hands will overlap every hour, but not on the hour. For example when it's 11:59, the hands will over lap in one minute on the 12. But When it's 12:59 you still have to wait 6 minutes before the hands overlap on the 1, becuase we cant forget that the hour hand moves too. So if you make a list, i think the times will be
12:00 am/pm
1:05 am/pm
2:10 am/pm
3:15 am/pm
4:20 am/pm
5:25 am/pm
6:30 am/pm
7:35 am/pm
8:40 am/pm
9:45 am/pm
10:50 am/pm
11:55 am/pm
That comes to a grand total of 24 times! |
|
That doesn't really work. For instance, for 3:15, the hour hand would have already moved a bit before the minute hand came to the digit 3. I'm pretty sure it overlaps 22 times, but I'm not sure how to find the exact times.
|
|
 IP Logged IP Logged |
|
|
|
Chewdog
Newbie


  
Gender: 
Posts: 50
|
 |
Re: Analog clock
« Reply #5 on: Jul 13th, 2003, 7:41pm » |
 Quote Quote  Modify Modify
|
Oh yea, i forgot that there is that little time where the hour hand moves slighlty.... but how did u come up with 22 times?
|
|
 IP Logged IP Logged |
|
|
|
James Fingas
Uberpuzzler
    


Gender: 
Posts: 949
|
 |
Re: Analog clock
« Reply #6 on: Jul 15th, 2003, 12:57pm » |
 Quote Quote  Modify Modify
|
There is a simple rigorous way to do this. First, notice that exactly the same thing happens in PM as in AM, so we'll consider how many times they overlap in a 12 hour period.
The minute hand moves 12 times around the clock, while the hour hand moves once around the clock. If you don't believe that the minute hand "passes" the hour hand 11 times just based on that, then choose X to be the hour hands' position (from zero to one), and write:
X = (12*X)%1
0 = (12*X)%1 - X
0 = (11*X)%1
While X goes from zero to 1, (11*X)%1 goes from zero to one 11 times, giving our expected answer of 11.
So in a 24 hour period, this happens twice, for a total of 22 times.
A better question is: how many times do the hour, minute, and second hands all overlap?
|
|
 IP Logged IP Logged |
Doc, I'm addicted to advice! What should I do?
|
|
|
Chewdog
Newbie


  
Gender: 
Posts: 50
|
 |
Re: Analog clock
« Reply #7 on: Jul 15th, 2003, 4:39pm » |
 Quote Quote  Modify Modify
|
Ok i know 24 times is wrong now, but one last thing.. I'm still not entirely convinced that it will overlap 22 times for one reason...
When you consider how many times the hands overlap in a 12 hour period and double your amount, you are leaving out one transition period. Condsidering it as a whole gives you a better look. Instead, now consider that the minute hand moves 24 times around the clock, while the hour hand moves once around the clock(two whole rotations for the day). This means they would overlap 23 times, not 22.
When you consider the overlaping times in a 12 hour period and double it, you leave out one over lap that comes when am turns to pm... I am pretty sure, i just need to get my hands on an analog clock to test it out
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Analog clock
« Reply #8 on: Jul 15th, 2003, 7:15pm » |
 Quote Quote  Modify Modify
|
You are counting the overlaps at both midnights - this is hardly fair to the surrounding days, one of which must settle for only 21 overlaps now! Why not be generous and share! Each day gets exactly 22 overlaps, instead of some getting more, and others getting less.
on Jul 15th, 2046, 8:16am, Moses wrote:
"When they measured it with an omer, he who had gathered much had no excess, and he who had gathered little had no lack; every man gathered as much as he should eat."
Exodus 16:18 |
|
|
| « Last Edit: Jul 16th, 2003, 4:00am by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Analog clock
« Reply #9 on: Jul 16th, 2003, 12:45am » |
 Quote Quote  Modify Modify
|
on Jul 15th, 2003, 7:15pm, Icarus wrote:| on Jan 1st, 1970, 12:59am, Moses wrote: |
|
I thought the bible was older than that 
so Moses was a hippie?
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Analog clock
« Reply #10 on: Jul 16th, 2003, 4:04am » |
 Quote Quote  Modify Modify
|
Alas, the date feature translates all dates before 1/1/70 (12/31/69 where I am at - apparently it's based on Coordinated Universal Time) to 1/1/70. 
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Chewdog
Newbie


  
Gender: 
Posts: 50
|
 |
Re: Analog clock
« Reply #11 on: Jul 21st, 2003, 11:18pm » |
 Quote Quote  Modify Modify
|
on Feb 13th, 2003, 12:26am, Nick wrote:Dear all,
One more, 2nd last one...
How many times each day do both the hour and minute hands overlap?
Nick |
|
on Jul 15th, 2003, 7:15pm, Icarus wrote:You are counting the overlaps at both midnights - this is hardly fair to the surrounding days, one of which must settle for only 21 overlaps now! Why not be generous and share! Each day gets exactly 22 overlaps, instead of some getting more, and others getting less.
|
|
I think that the riddle is asking how many times in each day do the hands overlap... not every day collectively. So I would assume that the riddle means how many times do they hands overlap from 12:00am to 11:59pm
|
|
 IP Logged IP Logged |
|
|
|
James Fingas
Uberpuzzler
    


Gender: 
Posts: 949
|
 |
Re: Analog clock
« Reply #12 on: Jul 22nd, 2003, 3:07pm » |
 Quote Quote  Modify Modify
|
An easy way to make sure you don't double-count anything is to count the number of overlaps from 12:05 to 12:05 or a similar 24-hour period. Counting the number of occurrances in an interval that has occurrances at both endpoints is unnecessarily confusing. Using this method, there's no question about how many overlaps occur per day.
You could even justify it, by reasoning that any clock is guaranteed to be slightly ahead of or slighly behind the "actual time".
|
|
 IP Logged IP Logged |
Doc, I'm addicted to advice! What should I do?
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Analog clock
« Reply #13 on: Jul 23rd, 2003, 5:07pm » |
 Quote Quote  Modify Modify
|
on Jul 21st, 2003, 11:18pm, Chewdogscp wrote:| I think that the riddle is asking how many times in each day do the hands overlap... not every day collectively. So I would assume that the riddle means how many times do they hands overlap from 12:00am to 11:59pm |
|
Yes, and if you count it that way, you will get 22 overlaps - that 23rd one you were getting is at 12:00 am again, after the end of your count. This was my point. Follow James' advice and you will see that the number is 22.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
somu
Newbie


Gender: 
Posts: 5
|
 |
Re: Analog clock
« Reply #14 on: Aug 12th, 2003, 7:07am » |
 Quote Quote  Modify Modify
|
I hope that the way of my calculation is correct :
Minute hand takes 3600 seconds to move 360 degree.
So its angular velocity = .1 degree/second
Minute hand takes 30 seconds to move 360 degree.
So its angular velocity = .0083 degree/second
So there relative velocity is .09167 degree/second as
they are moving in same direction.
At 1 o'clock the angle difference between these two
hands is 30 degree. So Minute-hand will take 30/.09167
second to touch hour-hand. i.e. 327.26 second (appx)
= 5 min 27 sec.
So its clear that they will meet next time right at
1:05:27.
keep calculating like that u will find the times ....
2:10:54
3:16:22
4:21:49
5:27:16
6:32:43
7:38:11
8:43:43
9:49:05
10:54:32
12:00
and total number or touch per day is obviously 22 
|
| « Last Edit: Aug 12th, 2003, 7:08am by somu » |
 IP Logged IP Logged |
|
|
|
abalagoo
Newbie


Posts: 3
|
 |
Re: Analog clock
« Reply #15 on: Sep 22nd, 2005, 12:21pm » |
 Quote Quote  Modify Modify
|
It is not hard to figure out the meet time after you getting the speed of the pointer.
Since the whole circle is devided into 12*5 = 60 units
1 hour, hour pointer "walks" 5 unites
1 hour, minute pointer "walks" 60 unites
their speed is 1/12 and 1. unit/mins
1*t-1/12*t=60 =>t = 12*60/11 =65.45mins
and so on.........
|
|
 IP Logged IP Logged |
|
|
|
algo_wrencher
Newbie


I am not insane, I enjoy every moment of it!
Posts: 44
|
 |
Re: Analog clock
« Reply #16 on: Sep 30th, 2005, 1:16pm » |
 Quote Quote  Modify Modify
|
Another easier way to visualize is:
The hands overlap at 12.
Next, they overlap in every angular sector between 2 consecutive numbers, per se between 2 and 3, between 3 and 4 and so on....but not between 12 and 1 and not between 11 and 12.
Which gives the no. of these "angular sectors" as 10.
10+1( at 12 ) =11.
Similarly for the other 12 hour period of the day and comes out to be 22 in totality..
|
|
 IP Logged IP Logged |
|
|
|
Aman1729
Newbie


Posts: 1
|
 |
Re: Analog clock
« Reply #17 on: May 13th, 2015, 12:15pm » |
 Quote Quote  Modify Modify
|
see this is a simple problem
the hour and minute hand of the clock cross each other
once between-
1. 11:00-1:00(NOTE:1 CROSSING ONLY AT 12:00 so we count it as the same day)
2. 1:00-2:00
3. 2:00-3:00
4. 3:00-4:00
5. 4:00-5:00
6. 5:00-6:00
7. 6:00-7:00
8. 7:00-8:00
9. 8:00-9:00
10. 9:00-10:00
11. 10:00-11:00
this makes it 11 crossings
now we will have 1 crossing again at 12 noon
and so on the patter continues.
we just take time till 11:59 as after that a new day starts(just as we included the previous 12:00 in this day we do the next 12:00 over here)
now, as the hands of the clock cross 11 times in 12 hours, this crossing repeats after every 12/11 hours.
and, we know that the hands cross at 12:00
so taking that into consideration we can find out the exact times of the crossings
12/11=1 1/11 hours
1/11 hrs=5.454545......mins
so the crossing occur at
12:00 and you keep adding 1 1/11 hrs so
12:00
1:5 454545 seconds
and so on it gets weird but this is the actual logic better to keep the seconds part in fraction
so 12
1 1/11 hr
2 2/11 hr
and so on
if it helps.....
|
|
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Analog clock
« Reply #18 on: May 16th, 2015, 10:07am » |
 Quote Quote  Modify Modify
|
on Jul 15th, 2003, 12:57pm, James Fingas wrote:| A better question is: how many times do the hour, minute, and second hands all overlap? |
|
Amazingly enough no answer to this question has been posted yet. Curiously enough 12 years later ...
The following (hopefully) visually intuitive sketch can be used as a template for all three cases:
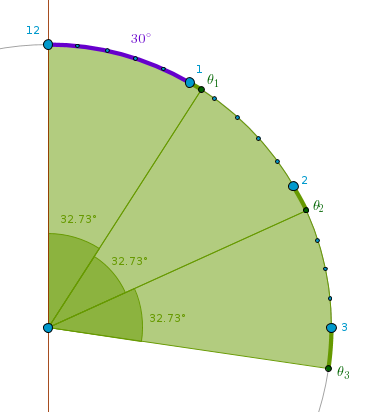
1). Minute/Hour hands rendezvous.
In physics two different types of motion described by the same mathematical equations are often called equivalent motions. When and if needed we can use this concept here. We can collapse the hands into (mathematical) points moving along the circumference of the clock's face at constant (interconnected) angular velocities. An angle  swept by such a point from some arbitrary initial position at a time t is: swept by such a point from some arbitrary initial position at a time t is:
 = =  t (1) t (1)
where  is an angular velocity. Assume the minute hand is at 12 sharp, the hour hand is at 1 sharp. For these two hands to meet two parameters must be the same - the angle is an angular velocity. Assume the minute hand is at 12 sharp, the hour hand is at 1 sharp. For these two hands to meet two parameters must be the same - the angle  both form with the vertical passing through 12 and 6 and the time t it took them to get to the rendezvous point. From (1): both form with the vertical passing through 12 and 6 and the time t it took them to get to the rendezvous point. From (1):
 1/360 = ( 1/360 = ( 1 - 1 1 - 1 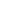 30)/30 = 30)/30 =  1/30 - 1 1/30 - 1
 1 = (360/11) 1 = (360/11) 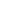 1 (2) 1 (2)
The sub index 1 designates the rendezvous after the 1-st hour, 360 =  m is the angular velocity of the minute hand (per hour), 30 = m is the angular velocity of the minute hand (per hour), 30 =  h - ditto the hour hand. For the p-th hour (p is some positive integer): h - ditto the hour hand. For the p-th hour (p is some positive integer):
 p = (360/11) p = (360/11) 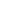 p (3) p (3)
Therefore when p = 11  11 = 360 - the full circle is complete, both hands point exactly at 12. Therefore 11 rendezvous per "half-day", 22 per "full day". 11 = 360 - the full circle is complete, both hands point exactly at 12. Therefore 11 rendezvous per "half-day", 22 per "full day".
2). Second/Hour hands rendezvous.
 s = 360 degrees per minute, s = 360 degrees per minute,  h = 0.5 degrees per minute: h = 0.5 degrees per minute:
 1/360 = ( 1/360 = ( 1 - 1 1 - 1 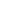 0.5)/0.5 = 0.5)/0.5 =  1/0.5 - 1 1/0.5 - 1
 1 = (360/719) 1 = (360/719) 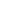 1 (4) 1 (4)
 q = (360/719) q = (360/719) 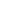 q (5) q (5)
where q is some positive integer. Therefore when q = 719  719 = 360 - the full circle is complete, both hands point exactly at 12. Therefore 719 rendezvous per "half-day", 1438 per "full day". 719 = 360 - the full circle is complete, both hands point exactly at 12. Therefore 719 rendezvous per "half-day", 1438 per "full day".
3). Second/Minute hands rendezvous.
 s = 360 degrees per minute, s = 360 degrees per minute,  m = 6 degrees per minute: m = 6 degrees per minute:
 1/360 = ( 1/360 = ( 1 - 1 1 - 1 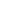 6)/6 = 6)/6 =  1/6 - 1 1/6 - 1
 1 = (360/59) 1 = (360/59) 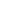 1 (6) 1 (6)
 r = (360/59) r = (360/59) 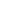 r (7) r (7)
where r is some positive integer. Therefore when r = 59  59 = 360 - the full circle is complete, both hands point exactly at 12. Therefore 59 rendezvous per hour, 708 per "half-day", 1416 per "full day". 59 = 360 - the full circle is complete, both hands point exactly at 12. Therefore 59 rendezvous per hour, 708 per "half-day", 1416 per "full day".
Since 11, 59 and 719 are all prime they are definitely relatively prime therefore the answer to the above question - all three hands rendezvous only once per "half-day" when they all point exactly at 12. Say we take (3) when the minute and hour hands meet. If we wish to make the second hand to overlap with these two we must find such q from (5) that:
p/11 = q/719
719/11 = q/p
Therefore p must be some multiple of 11 and from (3) it follows that  p must be some multiple of 360, which in the "hours speak" means 12 o'clock. Ditto q and 719. Conclusion - threesome twice per "full day" at 12 sharp. p must be some multiple of 360, which in the "hours speak" means 12 o'clock. Ditto q and 719. Conclusion - threesome twice per "full day" at 12 sharp.
|
|
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Analog clock
« Reply #19 on: May 16th, 2015, 10:19am » |
 Quote Quote  Modify Modify
|
While working through the above two more questions popped into my head:
4). At what times do all three hands are the closest to each other (barring 12 o'clock)?
5). I know that Grimbal may say "No, I did not!" but let us assume that at some random point during the day you looked at the 3-hand analog clock.
What is the probability that the second hand is closer to the minute/hour hand than it is to the hour/minute hand (pick your favorite combo).
Definition. Let MHAB be the Angular Bisector of the angle formed by the Minute and Hour hands. If the second and the minute hands are both on one side of MHAB then the second hand is closer to the minute hand. Ditto the hour hand.
(Let us keep Mr. Schrodinger and his cat out of this one)
|
|
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
5). As they say in US even a blind squirrel finds a nut once in a while. This problem turned out to be a delightful little mix of geometry, number theory and physics (and possibly something else). To not spoil the fun for the rest of the crowd let this be a fair warning: if you want to give it your own shot - do not read what follows.
The upcoming numbers can be obtained in a multitude of ways. To be consistent with my visual template, for example, we observe that at 12 sharp right before the hounds are released the angular distance between the second hand and the soon to be overtaken MHAB is 180 degrees since the second hand is way faster than the fastest object of the minute hand/MHAB/hour hand trio. No intersection of the second hand and MHAB right out of the gates:
Cutting to the chase and using the formulas from the previous post we get:
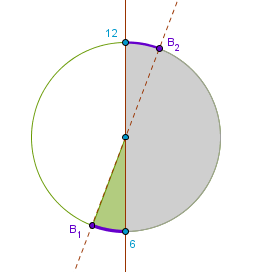
 n/360 = ( n/360 = ( n - 180 n - 180 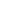 n)/(13/4) n)/(13/4)
 n = (360 n = (360 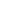 60 60 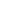 12 12 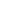 n)/1427 n)/1427
where 360*60*12 is the number of degrees spun by the second hand in a 12-hour period, n = 1, 2, 3, ... and 13/4 is the angular velocity of MHAB since it is an arithmetic average of the angular velocities of the minute and hour hands: (6 + 0.5)/2 degrees per hour. At B1 the situation will repeat as if B1 became a new 12, B2 - new 6 and B1B2 became a new 12/6 vertical rotated clockwise by a known number of degrees. And so on.
Therefore the second hand will intersect MHAB 1427 times where 1427 is prime. The total number of degrees spun by the second hand in 12 hours can be safely replaced with the number of seconds in the same period or 60*60*12 = 43200 in order to obtain the rendezvous times - not rendezvous angles.
Less computationally intensive but also less visual way of obtaining the same numbers is by using a little bit of physics. Let us move into the reference frame (RF) of the slowest moving object - the hour hand which, in the clock's face RF, runs at 1 unit per hour. Now the hour hand stands still, the clock's face runs counterclockwise at -1 unit per hour while the remaining objects run clockwise. The speed of the minute hand is now 12 - 1 = 11, the speed of the second hand is 12*60 - 1 = 719 and MHAB runs twice as slow as the minute hand at 11/2.
The second hand and MHAB now meet when the difference between the distances covered by both of them is some multiple of the half of the length of the circumference of the clock's face taken to be a unity:
(719 - 11/2) 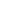 tn = n/2 tn = n/2
tn = n/(1438 - 11) = n/1427
In any case the entire 12-hour period is cut into the chunks of time when the second hand shares the half-circle delineated by MHAB with either the minute or the hour hand. Let us call the first state, when the second hand is closer to the minute hand, Green and let us call call the remaining state, when the second hand is closer to the hour hand, Red.
From the initial rendezvous observation it follows then that since 1427 is odd there will be 714 Green states and 713 Red. But that is not the full picture. Earlier we have proved that all three hands will never overlap during the 12-hour run except when all three point exactly at 12. Therefore during the 11 minute/hour hands rendezvous the second hand will be somewhere else within the Green or Red state and hence 11 10 times there will be an extra state switch. Since 11 10 is odd even 6 5 extra states will be Green and 5 more will be Red.
We now have the data to answer the question: let us call the sum of durations/angles of all the Green states the Green Sum and let us call the sum of durations/angles of all the Red states the Red Sum. The probabilities sought-after then are the ratios of the colored sums and the corresponding whole - time, 43200, or angles, 259200. In time units:
P(Green) = GreenSum/43200
P(Red) = RedSum/43200
I can see two types of solutions - brute force and analytic. The brute force solution is tedious and error-prone if done by hand and is better handled with software.
5.1). Brute Force Computer Program. The highlight of my algorithm in pseudo code (MHR = Minute/Hour hands Rendezvous):
precompute the 11 MHR times;
while ( elapsed time < 43200 )
{
if ( this time frame does not have the MHR )
{
add full time delta to the colored time;
}
else
{
add partial time delta to one colored time;
add remaining (full - partial) time delta to opposite colored time;
switch the state;
}
increment elapsed time;
move the time frame along;
switch the state;
}
subtract form last colored time the extra above 43200;
The output of my program is (request the C code if needed):
MHR:
01:05:27.272727273
02:10:54.545454545
03:16:21.818181818
04:21:49.090909091
05:27:16.363636364
06:32:43.636363636
07:38:10.909090909
08:43:38.181818182
09:49:05.454545455
10:54:32.727272727
12:00:00.000000000
fulldelta = 30.273300631
green tm = 21601.376059 N = 719
red tm = 21598.623941 N = 718
green tm + red tm = 43200.000000
green tm - red tm = 2.752118235
last state was green
P(green) = 0.500031853
P(red) = 0.499968147
The output should be self explanatory. The variable fulldelta is 43200/1427 and N captures the number of colored states.
[e]
Silly mistakes corrections (see above).
Attached a copy of my program (as is, no warranties). To build it: gcc -g -o ac ac.c
[/e]
|
| « Last Edit: May 23rd, 2015, 5:12pm by rloginunix » |
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Analog clock
« Reply #21 on: May 22nd, 2015, 4:30pm » |
 Quote Quote  Modify Modify
|
5.2). For an analytic solution geometry comes in handy:
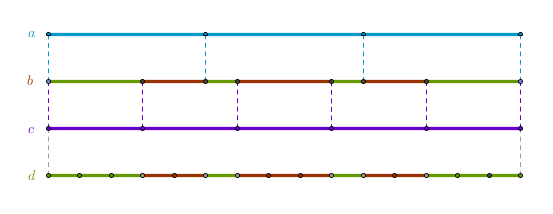
The line segment a represents the division of the entire 12-hour time frame (taken to be a unity) in p = 3 (11 implied) equal pieces when the state flips due to the minute/hour hands rendezvous.
The line segment c represents the division of the frame in q = 5 (1427 implied) equal pieces when the state flips due to the second hand/MHAB rendezvous.
The line segment b is a geometric superposition of a and c. I used it to write the C code. However, this line segment is not convenient for summation.
Here we observe that 11 and 1427 are odd primes. Therefore they are relatively prime and gcd(11, 1427) = 1. From gcd(p, q)*lcm(p, q) = p*q it follows then that lcm(11, 1427) = 11*1427 = 15697. Therefore the division lines on b will never coincide and therefore if we divide the unity long frame into p*q = 15697 equally sized pieces - depicted as a line segment d - two things will occur:
1). each piece will obviously have the same length and 2). each piece will be of only one color. Together, 1) and 2) form some sort of a pattern using which the sum should be analytically calculable.
By experimenting with the smallest odd primes we see that the number of Green pieces in the above 3x5 case is 8 and the number of Red pieces is 7. For a 3x7 case we get 11 Green and 10 Red. I do not have a rigorous proof yet but the conjecture is that the colored counts fall on the dead geometric "center" of the p*q-divided segment. Since the numbers are odd we add 1 to the whole to get the Green count: (3*5 + 1)/2 and we subtract 1 from the whole to get the Red count: (3*5 - 1)/2 and 1 gets lost in the shuffle. Therefore for p = 11 and q = 1427 the probabilities are:
P(green) = (11*1427 + 1)/(2*11*1427) = 7849/15697 = 0.500031853
P(red) = (11*1427 - 1)/(2*11*1427) = 7848/15697 = 0.499968147
So the conjecture (proof pending) is:
for any pair of positive odd prime integers p, q (p<q) the sum of Green pieces is (p*q + 1)/2 while the sum of Red pieces is (p*q - 1)/2 for a line segment of length 1 cut into p*q pieces of equal length in the analog clock hands and the minute/hour hands bisector rendezvous formation.
I think the conjecture can be relaxed to any pair of odd relatively prime positive integers.
I will be working on a proof but if someone has it already - feel free to share.
|
|
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Analog clock
« Reply #22 on: May 28th, 2015, 5:45pm » |
 Quote Quote  Modify Modify
|
John Nash who unfortunately just recently perished in a car accident mentioned shortly before his tragic demise that in math it is more important to learn how to relax one's brain instead of tensing it. Similarly Carl Gauss reasoned that one should step back from a problem for a solution to reveal itself.
A number of failures preceded the following find. At first, for example, I've tried to inscribe the regular 3- and 5-gons into a circle of radius 1, construct a circle of radius 2, to every point P on a 1-circle's circumference correlate a point P' on the 2-circle's circumference such that the central angle through P' and the 12 o'clock mark is half the corresponding angle for P. Basically, compress the 1-circle onto the 2-circle. The arc lengths will then be the same, etc. Did not work out.
Turns out multiplication is the essence of
5). The proof.
Let 1<p< q, gcd(p, q) = 1, p = 2k + 1, q = 2r + 1.
Cut the line segment a into p equal pieces. Alternate their colors. Cut each 1/p piece into q equal pieces for a total of pq. Assign +1 to each Green piece and -1 to each Red piece. Fold a into a p  q rectangle A. Fill its cells with the corresponding +1s and -1s. q rectangle A. Fill its cells with the corresponding +1s and -1s.
Swap p and q. Repeat.
Rotate any one of two rectangles in any direction 90 degrees. Create a third blank p  q rectangle. Fill its cells with an algebraic product of two corresponding cells from A and C - plus times plus or minus times minus equals a plus, etc: q rectangle. Fill its cells with an algebraic product of two corresponding cells from A and C - plus times plus or minus times minus equals a plus, etc:
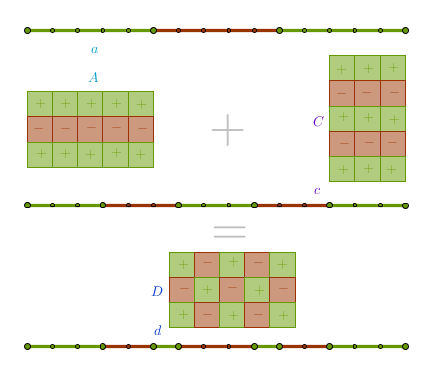
The resulting rectangle D will resemble a funky chess board. Pick any direction, p (vertical) or q (horizontal). Say we pick p. Since it is odd (p - 1) is even. Therefore pairwise each of the top (p - 1)/2 row by row sums sums to 0. The remaining bottom row, horizontally, sums to 1:
GreenSum + RedSum = pq
GreenSum - RedSum = 1
Add the two equations. Solve for GreenSum and then for RedSum:
GreenSum = (pq + 1)/2
RedSum = (pq - 1)/2
What was required to prove.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register