Author |
Topic: William the Logger (Read 502 times) |
|
rloginunix
Uberpuzzler
Posts: 1029
|
 |
William the Logger
« on: Apr 1st, 2015, 6:43pm » |
 Quote  Modify
|
William the Logger.
Down the Math River that has parallel banks and a width a Willy Wu is floating logs which can be approximated as absolutely rigid line segments. At some point the river makes a ninety-degree turn and while its banks remain parallel its width is now b:
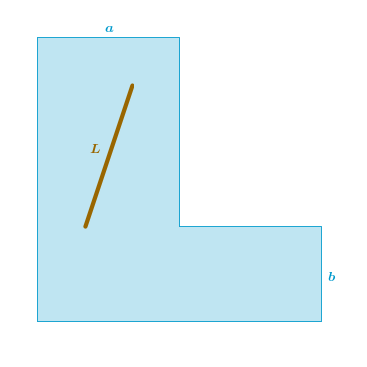
For a given a and b what is the longest log L can William safely float around the bend in such a way that the log does not get bent, broken, stuck, submerged below or popped above water (when only 2-dimensional transformations are allowed)?
Put it another way. If William knows a, b and L ahead of time when should he make the trip?
|
|
 IP Logged |
|
|
|
jollytall
Senior Riddler
Gender: 
Posts: 585
|
|
Re: William the Logger
« Reply #1 on: Apr 1st, 2015, 9:45pm » |
Quote Modify
|
First idea:
Make the log in alpha degree compared to the horizontal line, when it is almost stuck. Then the "corner" splits it into two parts, x across river a and y across river b.
x*cos(alpha) = a
y*sin(alpha) = b
The log is a/cos(alpha)+b/sin(alpha)
The minimum of it is when the derivative is 0, i.e.
-a*cos(alpha)/sin2(alpha)+b*sin(alpha)/cos2(alpha)=0.
tg(alpha) = (a/b)^(1/3)
From alpha x+y = L can be calculated.
|
|
IP Logged |
|
|
|
pex
Uberpuzzler
Gender:
Posts: 880
|
|
Re: William the Logger
« Reply #2 on: Apr 1st, 2015, 10:06pm » |
Quote Modify
|
on Apr 1st, 2015, 9:45pm, jollytall wrote:First idea:
Make the log in alpha degree compared to the horizontal line, when it is almost stuck. Then the "corner" splits it into two parts, x across river a and y across river b.
x*cos(alpha) = a
y*sin(alpha) = b
The log is a/cos(alpha)+b/sin(alpha)
The minimum of it is when the derivative is 0, i.e.
-a*cos(alpha)/sin2(alpha)+b*sin(alpha)/cos2(alpha)=0.
tg(alpha) = (a/b)^(1/3)
From alpha x+y = L can be calculated. |
|
That's pretty much what I did. The result is rather cute: L = (a2/3 + b2/3) 3/2.
|
|
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: William the Logger
« Reply #3 on: Apr 2nd, 2015, 9:28am » |
Quote Modify
|
You guys are both correct and what is rather amazing is that I took exactly the same route. Interesting.
There is also a more analytic (academic) approach, if you will: the orthogonal banks are actually the XOY axes. The log must slide along both playing a role of a tangent to some curve. So the question is - find the curve the length of tangent to which trapped between the axes is constant at all times. If the (a,b) corner is inside that curve - no go. Pythagoras and an equation of a straight line lead to a differential equation in this case.
Turns out that the equation given by pex describes a curve known as astroid.
Well done.
(I interpreted jollytall's last equation like so: tg( ) is almost a derivative, for it to be a real one the angle must be  - and then we get a trivial differential equation dy/dx = -(y/x)1/3 ...)
PS
This particular puzzle interconnects with A Cat on a Ladder and Infinite Fast Ladder in the easy section.
[edit]
Fixed two spelling errors.
[/edit]
|
| « Last Edit: Apr 2nd, 2015, 11:50am by rloginunix » |
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print