Author |
Topic: 401 Circles (Read 4273 times) |
|
BMAD
Junior Member
Posts: 57
|
 |
401 Circles
« on: May 23rd, 2014, 6:18am » |
 Quote  Modify
|
In a rectangle that's 2 by 200 units long, it's trivial to draw 400 non-overlapping unit-diameter circles.
But in the same rectangle, can you draw 401 circles?
|
|
 IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender: 
Posts: 13730
|
|
Re: 401 Circles
« Reply #1 on: May 23rd, 2014, 8:40am » |
Quote Modify
|
Seems doable. You can group three circles as triangle and then pack them alternately with a side to the top and bottom. This gives a little bit of space along the long axis, which should be enough to both offset the initial cost and the cost of adding an extra circle. Though I haven't done the calculations.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: 401 Circles
« Reply #2 on: May 23rd, 2014, 9:37am » |
Quote Modify
|
The area of an "elementary" square is 4. The total area of four circles is Pi (3.14). Of course can't go by area but the star-looking shape in the dead center of the square looks wasteful:
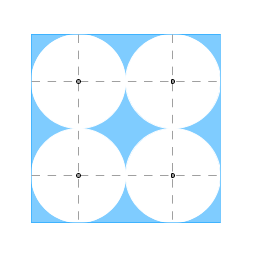
Was also thinking along those lines - throw out the fourth circle and group them by three instead.
Kinda busy right now to do the math ...
|
|
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: 401 Circles
« Reply #3 on: May 23rd, 2014, 10:04am » |
Quote Modify
|
I think you should start with 1 circle top left (assuming a horizontal rectangle), then only 3 in a triangle along the bottom edge, 3 top, 3 bottom, etc
|
| « Last Edit: May 23rd, 2014, 10:06am by Grimbal » |
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: 401 Circles
« Reply #4 on: May 23rd, 2014, 1:41pm » |
Quote Modify
|
I can fit a basic rectangle-fitted unit of 3 circles (two halved) into a length of sqrt(sqrt(3) - 3/4)+1/2 ~= 1.491, so that gives ~198.3 for 399 circles, with a halved circle at each end. So adding two halves and a whole (with some overlap in x dimension), that comes to ~ 199.8 for 401 circles
|
| « Last Edit: May 23rd, 2014, 1:45pm by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: 401 Circles
« Reply #5 on: May 23rd, 2014, 3:36pm » |
Quote Modify
|
It looks like you can already fit one more circle starting with size 167.
|
|
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: 401 Circles
« Reply #6 on: May 25th, 2014, 11:51am » |
Quote Modify
|
With these assumptions: 1). the circles are hard, 2). no overlapping is allowed, 3). the circles can't be cut up, they must remain wholesome, 4). the circles are not heated prior to packing, this is what I get:
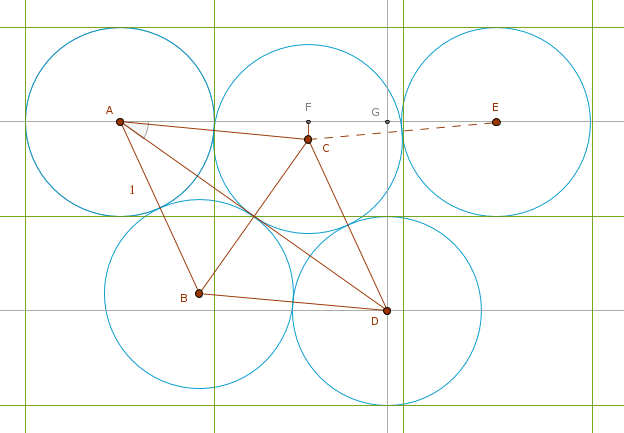
From two right triangles forming the triangle ABD we get (Pythagoras):
AD = 2*sqrt(1 - 1/4) = sqrt(3)
From the right triangle AGD we get:
AG = sqrt(AD^2 - GD^2) = sqrt(3 - 1) = sqrt(2)
angle DAG = arccos(AG/AD) = arccos(sqrt(2/3)) = 35.26438968 degrees
angle CAG = angle DAG - 30 = 5.26438968 degrees
From the right triangle AFC we get:
AF = AC*cos 5.26438968 = 1*cos 5.26438968 = 0.995781916 < 1
Basically, with this packing we see that the centers of the top circles move left bit by bit. The center of the top third circle centered at E is not 2 units away from A but:
AE = 2*AC*cos 5.26438968 = 1.991563832
units away from A. So the center of every top circles moves left by delta = 1 - 0.995781916 = 0.004218084 of one unit.
So the question is after how many such moves the delta will grow to be exactly 1 unit so that we can fit 1 extra circle in the top row:
delta*x = 1
x = 1/delta = 1/0.004218084 = 237.074463192
Rounded up it becomes 238. So it looks like in a rectangular formation of 2x238 we can fit 2*238 + 1 = 477 hard non-overlapping not heated wholesome circles with 238 being the smallest column count large enough to accommodate one extra circle. Rewording in an independent form, n = 119 (238/2) for 4n + 1 above circles to fit in the 2 by 2n given rectangular formation.
What am I missing?
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: 401 Circles
« Reply #7 on: May 25th, 2014, 12:50pm » |
Quote Modify
|
You're missing a better way to pack the circles.
Cut the connection between A and B, let gravity do its work and pull B,C,D down, A and E move closer together. Profit!
|
| « Last Edit: May 25th, 2014, 12:51pm by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: 401 Circles
« Reply #8 on: May 25th, 2014, 6:07pm » |
Quote Modify
|
Thank you, towr ... and now that I am sober:
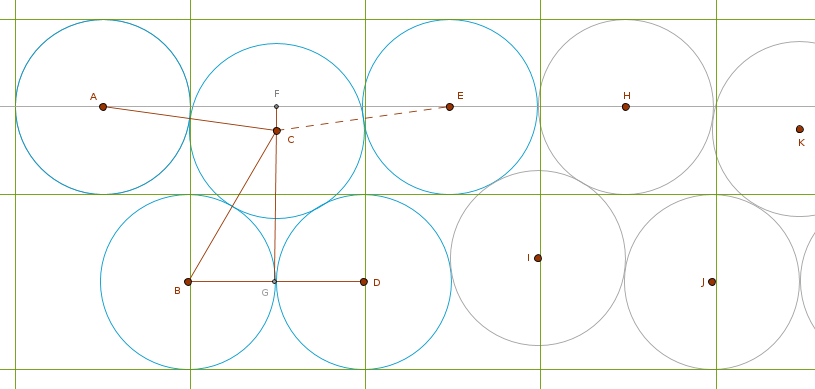
FC = FG - CG = 1 - sqrt(1 - 1/4) = 1 - sqrt(3)/2 = 0.133974596
CG is calculated from the right triangle BGC and Pythagoras. From the right triangle AFC we have:
AF = sqrt(AC^2 - FC^2) = sqrt(1 - 0.017949192) = sqrt(0.982050808) = 0.990984767
So the C circle's horizontal drift is 1 - 0.990984767 = 0.009015233 and the E circle's horizontal drift is double that: 0.018030466.
As we can see we have the Olympic rings pattern at work - the grayed out circles H, K, J are the images of the circles A, C, B correspondingly. So we only gain the delta of 0.018030466 every third unit square. After delta*N unit squares we want to gain 1 extra:
delta*N = 1
N = 1/delta = 1/0.018030466 = 55.461683575
But since its every third unit gain we must multiply the above number by 3:
x = N*3 = 55.461683575*3 = 166.385050725
Rounding it up we get 167. So after the 167-th unit square we can add one more circle to the rectangle.
P.S.
In the hind sight the common "three grouping" hunch was correct.
The hypocycloid-shaped negative space of the original 4-circle formation became a flip flopping much sqooshed hypocycloid trapped between the circles C, D, I, E and H, K, J, I.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print