 Author
Author |
Topic: Random movement probability problem (Read 1532 times) |
|
marsh8472
Newbie


Posts: 27
|
 |
Random movement probability problem
« on: Sep 16th, 2012, 5:21am » |
 Quote Quote  Modify Modify
|

A dog is put in the backyard on a leash that is L units long. Every second a dog moves 1 unit in a randomly picked direction (any real number from 0 to 360 degrees). What is the probability that this dog will reach the end of its leash at least once within the first X seconds?
|
| « Last Edit: Sep 16th, 2012, 5:30am by marsh8472 » |
 IP Logged IP Logged |
|
|
|
marsh8472
Newbie


Posts: 27
|
 |
Re: Random movement probability problem
« Reply #1 on: Sep 16th, 2012, 6:19am » |
 Quote Quote  Modify Modify
|
There's probably recursion and integration involved with this
Coordinates after X seconds =
(0,0), if X=0
Coordinates after X-1 seconds + (cos(random), sin(random)), if X>0
|
| « Last Edit: Sep 16th, 2012, 6:19am by marsh8472 » |
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Random movement probability problem
« Reply #2 on: Sep 16th, 2012, 6:53am » |
 Quote Quote  Modify Modify
|
I think the following recursion should describe the solution, but it doesn't seem very useful for anything other than finding numerical solutions to specific cases.
F(L,d,x) = 1 if d  L or d L or d  -L -L
F(L,d,0) = 0 if -L < d < L
F(L,d,x) = 1/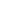    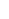 0 F(L, |d + e 0 F(L, |d + e 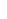 |, x-1 ) d |, x-1 ) d  if -L < d < L and x > 0 if -L < d < L and x > 0
|
| « Last Edit: Sep 16th, 2012, 6:54am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register