Author |
Topic: marmelade jars (Read 1969 times) |
|
Altamira_64
Junior Member
Posts: 116
|
 |
marmelade jars
« on: Apr 17th, 2012, 3:40pm » |
 Quote  Modify
|
There are 5 closed marmelade jars one next to the other. One of them contains a whole walnut, which you are trying to locate. You start by opening each jar. Once you find which jar it is in, you win the game. However, if you do not find the nut, it is somehow (in a magic, invisible way!) moved to one of the adjacent boxes (for example, if the walnut was initially in the jar No 2, it is then moved to jar No 1 or No 3). Is there any strategy by which you always win the game and what is the maximum number of tries it will take you?
|
| « Last Edit: Apr 17th, 2012, 3:42pm by Altamira_64 » |
 IP Logged |
|
|
|
MacNCheese
Newbie
Gender: 
Posts: 9
|
|
Re: marmelade jars
« Reply #1 on: Apr 17th, 2012, 4:20pm » |
Quote Modify
|
"You start by opening each jar"
Does this mean we get to leave the jars open? Because then I would just corner the walnut by going in one direction 
I'm guessing not, so one solution is obviously to repeatedly open a particular jar. It will eventually contain the walnut in it. I haven't put much thought in it yet, but I suppose it's like predicting a random walk.
|
|
IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender: 
Posts: 2084
|
|
Re: marmelade jars
« Reply #2 on: Apr 17th, 2012, 6:30pm » |
Quote Modify
|
Open the jars in the following order: 2, 2, 3, 4, 5. If you don't find it on the first guess, you know that jar 1 is now empty, since if the nut was in jar 1 it must have moved to jar 2, and the only place it could have moved into jar 1 from is jar 2 which you opened. The next guesses rule out successive jars until you find the nut.
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
MacNCheese
Newbie
Gender:
Posts: 9
|
|
Re: marmelade jars
« Reply #3 on: Apr 18th, 2012, 6:51am » |
Quote Modify
|
@SMQ
I don't think that would work all the time. A counterexample:
Say the walnut is in jar 4. You open 2(empty), it goes to 5. You open 2 again(empty), it goes back to 4. You open 3(empty), it goes to 5. You open 4(empty), it goes to 4. You open 5 and it's empty.
|
|
IP Logged |
|
|
|
fieldazed
Junior Member
Gender:
Posts: 55
|
|
Re: marmelade jars
« Reply #4 on: Apr 18th, 2012, 6:59am » |
Quote Modify
|
some thoughts - seven seems to be the obvious answer with several ways of going about it. think it can be done in six peeks - 2,3,4,2,3,4 but seems it should be doable in five.
|
|
IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: marmelade jars
« Reply #5 on: Apr 18th, 2012, 12:48pm » |
Quote Modify
|
With a bit more investigation, it appears the game with n jars (where n > 2) is minimally winnable in 2(n - 2) moves by playing (2, 3, ..., n - 1, n - 1, n - 2, ..., 2) (or its mirror image). Iff n is odd, you can alternately play (2, 3, ..., n - 1, 2, 3, ..., n - 1) (or its mirror) as fieldazed discovered.
(The games with 0, 1, and 2 jars are trivially winnable by playing 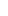 , 1, and (1, 1) respectively.)
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
MacNCheese
Newbie
Gender:
Posts: 9
|
|
Re: marmelade jars
« Reply #6 on: Apr 18th, 2012, 1:16pm » |
Quote Modify
|
Wow. Interesting. How would you go about proving it for n jars though?
|
|
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2873
|
|
Re: marmelade jars
« Reply #7 on: Apr 18th, 2012, 2:45pm » |
Quote Modify
|
on Apr 18th, 2012, 1:16pm, MacNCheese wrote:| Wow. Interesting. How would you go about proving it for n jars though? |
|
I'd switch it from a 1+1 dimensional problem to a 2 dimensional problem - rather than having a row of jars changing with time, have an array of jars where each row has a walnut in one jar, diagonally adjacent to the neighbouring rows'.
You can then label the jars with "black" and "white" chessboard-style and it should be obvious that the walnuts must either all be in black jars or all in white. If 2 starts off black, then going from there on the diagonal must find a walnut if they're on black - and do it by the time you reach (n-1) at the latest - the walnuts can't start to the left and still be black, can't cross your diagonal without you finding them, and can't still be to the right once you open (n-1) and still be black. (n-1) in the next row must be white and sweeping diagonally left eliminates the possibility of it being white in the same way.
|
|
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
Gender:
Posts: 2873
|
|
Re: marmelade jars
« Reply #8 on: Apr 18th, 2012, 2:57pm » |
Quote Modify
|
An interesting extension I've encountered is to consider what other layouts the problem is solvable for - if, instead of putting the jars in a straight line, you scatter them and run strings between them to form some kind of web and the walnut only moves along the strings, always stopping at the first jar it reaches each time, for what webs can the walnut be guaranteed to be found within a finite number of moves?
|
|
IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: marmelade jars
« Reply #9 on: Apr 18th, 2012, 3:09pm » |
Quote Modify
|
on Apr 18th, 2012, 2:45pm, rmsgrey wrote:| I'd switch it from a 1+1 dimensional problem to a 2 dimensional problem - rather than having a row of jars changing with time, have an array of jars where each row has a walnut in one jar, diagonally adjacent to the neighbouring rows'. |
|
Or, equivalently, a single walnut moves from bottom to top of the chessboard, always moving diagonally forward (a chess pawn's attack), and you can place one fence piece in each row to attempt to stop it. I think that construction makes the minimality of the construction easier to visualize, as any fewer rows must leave a gap in the fence.
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print