 Author
Author |
Topic: Interval Inequality (Read 1137 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Interval Inequality
« on: Aug 23rd, 2010, 7:27am » |
 Quote Quote  Modify Modify
|
Two numbers, a and b, are randomly chosen, the first (a) from the interval [0, 0.5] and the second (b) from the interval [0.5, 1].
For n 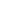 2, what is the probability that b 2, what is the probability that b 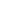 na? na?
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: Interval Inequality
« Reply #1 on: Aug 23rd, 2010, 7:32am » |
 Quote Quote  Modify Modify
|
Expecting uniform distribution the question can be reformulated as a is chosen from interval [0,n/2] .... or scaled twice more a from [0,n] b from [1,2].
There are 3 cases ... a<1, a belongs to [1,2] and a>2 ...
|
| « Last Edit: Aug 23rd, 2010, 7:36am by Hippo » |
 IP Logged IP Logged |
|
|
|
TenaliRaman
Uberpuzzler
    

I am no special. I am only passionately curious.
Gender: 
Posts: 1001
|
 |
Re: Interval Inequality
« Reply #2 on: Aug 23rd, 2010, 8:25am » |
 Quote Quote  Modify Modify
|
0.1875 * 4 = 0.75 for n = 2
Edit : Reconsidering after towr's post. Realized that I had done it for a specific case of n = 2. Also fixed a bug (had divided by the wrong area)
-- AI
|
| « Last Edit: Aug 23rd, 2010, 8:57am by TenaliRaman » |
 IP Logged IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Interval Inequality
« Reply #3 on: Aug 23rd, 2010, 8:37am » |
 Quote Quote  Modify Modify
|
Uh.. what? Shouldn't it depend on n, Tenali?
I get:
a=x/2
b=y/2+1/2
a < b
n/2*x < y/2+1/2
x < (y+1)/n
int_0^1 (y+1)/n dy
(y^2/2+y)/n|_0^1
1.5/n
It seems to fit with experimental results, but it can't be right for n=1.5, even though I think it should (not that it's asked)... [edit]Ah no wait, I think I figured it out.. then we should integrate max( (y+1)/n, 1)[/edit]
|
| « Last Edit: Aug 23rd, 2010, 8:45am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Interval Inequality
« Reply #4 on: Aug 23rd, 2010, 9:07am » |
 Quote Quote  Modify Modify
|
The original problem has n an integer 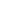 2, but n real and 2, but n real and 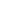 3/2 is sufficient, I think. 3/2 is sufficient, I think.
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Interval Inequality
« Reply #5 on: Aug 23rd, 2010, 9:10am » |
 Quote Quote  Modify Modify
|
You need n >= 2 to keep it simple. Otherwise any n would work, although it's just 1 for n<=1.
[edit]For 1<n<2 P(b > an) = 2-(n2+1)/(2n) [/edit]
|
| « Last Edit: Aug 23rd, 2010, 9:22am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Interval Inequality
« Reply #6 on: Aug 23rd, 2010, 9:38am » |
 Quote Quote  Modify Modify
|
on Aug 23rd, 2010, 8:25am, TenaliRaman wrote:0.1875 * 4 = 0.75 for n = 2
|
|
That is correct.
And for n > 2 the same sort of shapes are involved, right?
|
| « Last Edit: Aug 23rd, 2010, 9:40am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
TenaliRaman
Uberpuzzler
    

I am no special. I am only passionately curious.
Gender: 
Posts: 1001
|
 |
Re: Interval Inequality
« Reply #7 on: Aug 23rd, 2010, 12:51pm » |
 Quote Quote  Modify Modify
|
on Aug 23rd, 2010, 9:38am, ThudanBlunder wrote:
That is correct.
And for n > 2 the same sort of shapes are involved, right?
|
|
Yeah, a rectangle at the bottom with a triangle on top
Edit : Ok, I tried to generalize the idea for any n. I might be doing something wrong here because I am getting a different answer than towr.
Edit2 : Found the error
-- AI
|
| « Last Edit: Aug 23rd, 2010, 1:43pm by TenaliRaman » |
 IP Logged IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
TenaliRaman
Uberpuzzler
    

I am no special. I am only passionately curious.
Gender: 
Posts: 1001
|
 |
Re: Interval Inequality
« Reply #8 on: Aug 23rd, 2010, 1:56pm » |
 Quote Quote  Modify Modify
|
Just documenting the method I used here -
The method is same as what gets used in meeting probability solution (which is not much different from what towr has done).
Let us represent the two random variables on the two axis, just as was done for the Meeting Probability. However, the intervals on the x and y axis this time would be (0,1). This gives us a unit square. Since, a takes values in (0, 0.5) and b takes values in (0.5,1), our sample space is the fourth quadrant (i.e if you divide the unit square into four equal halves).
Now, given an 'n', shade the event space. The shaded space would be :
1] a rectangle of height (0.5/n) and
2] a triangle on top of the rectangle of height ((1/n) - (0.5/n))
Computing the area of this shaded region would give you : (0.25) * (3/(2n))
The area of the sample space is 0.25, so the probability comes out to 3/(2n) or 1.5/n.
-- AI
P.S. -> Yeah, a diagram like Wu's would have been really useful here 
|
|
 IP Logged IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Interval Inequality
« Reply #9 on: Aug 23rd, 2010, 2:03pm » |
 Quote Quote  Modify Modify
|
on Aug 23rd, 2010, 8:37am, towr wrote:
It seems to fit with experimental results, but it can't be right for n=1.5, even though I think it should (not that it's asked)... [edit]Ah no wait, I think I figured it out.. then we should integrate max( (y+1)/n, 1)[/edit] |
|
Can't we avoid nuking a gnat by considering the square formed by the points
(0, 0.5)
(0, 1.0)
(0.5, 0.5)
(0.5, 1.0)
and its intersection with the line y = nx?
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Interval Inequality
« Reply #10 on: Aug 23rd, 2010, 2:57pm » |
 Quote Quote  Modify Modify
|
I don't think that's really different from what I end up doing. If you split up the parts of the integral right*, the only significant difference is that using an integral is a silly way to calculate the area of a triangle; for the rectangular parts it makes no difference.
*(You can just split the integral at the point where (y+1)/n=1 to do away with the max function.)
|
| « Last Edit: Aug 23rd, 2010, 2:58pm by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register