wu :: forums « wu :: forums - Trignometric Recurrence » Welcome, Guest. Please Login or Register. Nov 24th, 2024, 5:56pm

RIDDLES SITE WRITE MATH! Home Help Search Members Login Register

wu :: forums    riddles    medium (Moderators: william wu, towr, Icarus, ThudnBlunder, Eigenray, Grimbal, SMQ)    Trignometric Recurrence « Previous topic | Next topic » Pages: 1  Reply Notify of replies Send Topic Print    Author  Topic: Trignometric Recurrence  (Read 671 times) ThudnBlunder wu::riddles Moderator Uberpuzzler The dewdrop slides into the shining Sea     Gender: Posts: 4489 Trignometric Recurrence   « on: Aug 1st, 2010, 12:41pm » Quote Modify If u1 = 1 and un+1 = cos[arctan(un)] for n 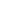1, find a formula for un. IP Logged THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you. towr wu::riddles Moderator Uberpuzzler Some people are average, some are just mean.     Gender: Posts: 13730 Re: Trignometric Recurrence   « Reply #1 on: Aug 1st, 2010, 1:45pm » Quote Modify Using cos(atan(x)) = 1/sqrt(x2+1) Take vn = u2n Then vn+1 = 1/(vn + 1)  => convergents for phi-1 In other words, vn+1 = F(n)/F(n+1) So, un = sqrt( F(n)/F(n+1) ) « Last Edit: Aug 1st, 2010, 1:46pm by towr » IP Logged Wikipedia, Google, Mathworld, Integer sequence DB Pages: 1  Reply Notify of replies Send Topic Print Forum Jump: ----------------------------- riddles -----------------------------  - easy => medium   - hard   - what am i   - what happened   - microsoft   - cs   - putnam exam (pure math)   - suggestions, help, and FAQ   - general problem-solving / chatting / whatever ----------------------------- general -----------------------------  - guestbook   - truth   - complex analysis   - wanted   - psychology   - chinese « Previous topic | Next topic »

Powered by YaBB 1 Gold - SP 1.4!
Forum software copyright © 2000-2004 Yet another Bulletin Board