 Author
Author |
Topic: Radically Constant (Read 966 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Radically Constant
« on: Aug 1st, 2010, 9:24am » |
 Quote Quote  Modify Modify
|
Find numbers a and b (a < b) and the value of the constant such that
[x + 2 (x - 1)]1/2 + [x - 2 (x - 1)]1/2 + [x - 2 (x - 1)]1/2 is constant for a (x - 1)]1/2 is constant for a 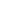 x x 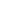 b. b.
|
| « Last Edit: May 19th, 2011, 4:42am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Radically Constant
« Reply #1 on: Aug 2nd, 2010, 1:26am » |
 Quote Quote  Modify Modify
|
 [x + 2 [x + 2  (x - 1)] + (x - 1)] +  [x - 2 [x - 2  (x - 1)] = c (x - 1)] = c
 [x + 2 [x + 2  (x - 1)] = c - (x - 1)] = c -  [x - 2 [x - 2  (x - 1)] (x - 1)]
x + 2  (x - 1) = c2 - 2c (x - 1) = c2 - 2c  [x - 2 [x - 2  (x - 1)] + x - 2 (x - 1)] + x - 2  (x - 1) (x - 1)
4  (x - 1) = c2 - 2c (x - 1) = c2 - 2c  [x - 2 [x - 2 (x - 1)] (x - 1)]
4  (x - 1) - c2 = - 2c (x - 1) - c2 = - 2c  [x - 2 [x - 2 (x - 1)] (x - 1)]
16 (x - 1) - 8c2  (x - 1) + c2 = 4c2 [x - 2 (x - 1) + c2 = 4c2 [x - 2 (x - 1)] (x - 1)]
16 (x - 1) + c^4 = 4 c2 x
take c2 = y
y2 - 4 y x + 16 (x - 1) = 0
y = [4x +/-  (16x2 - 64 (x - 1)) ]/2 (16x2 - 64 (x - 1)) ]/2
y = 2(x +/-  ((x-2)2))) ((x-2)2)))
y = 2(x +/- (x-2))
If y is constant, than y must be 4, so c is +/- 2
From the graph it's easy to see that a = -inf, b=2, c=2, but I'm going to have to take a raincheck on trying to proof it.
|
| « Last Edit: Aug 2nd, 2010, 1:40am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
0.999...
Full Member
  

Gender: 
Posts: 156
|
 |
Re: Radically Constant
« Reply #2 on: Aug 2nd, 2010, 5:43am » |
 Quote Quote  Modify Modify
|
If we have a real function f(x) =  [x+2 [x+2 (x-1)] + (x-1)] +  [x-2 [x-2 (x-1)] then it is defined only for values of x (x-1)] then it is defined only for values of x  1. 1.
Let m =  (x-1). Hence, f(x) = (x-1). Hence, f(x) =  (m2+2m+1) + (m2+2m+1) +  (m2-2m+1) = |m+1|+|m-1| = 2 (m2-2m+1) = |m+1|+|m-1| = 2 (x-1) if x (x-1) if x  2. 2.
On the other hand, if 1  x x  2, then m+1 2, then m+1  0 and m-1 0 and m-1  0. So f(x) = m+1-(m-1) = 2. 0. So f(x) = m+1-(m-1) = 2.
Hence a = 1, b = 2, f(x) = 2 in this interval.
|
| « Last Edit: Aug 2nd, 2010, 6:31am by 0.999... » |
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Radically Constant
« Reply #3 on: Aug 2nd, 2010, 7:02am » |
 Quote Quote  Modify Modify
|
But the function as a whole is both real and 2 for x < 1.
The only problem there is if you want sqrt to be a real function.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
0.999...
Full Member
  

Gender: 
Posts: 156
|
 |
Re: Radically Constant
« Reply #4 on: Aug 2nd, 2010, 7:12am » |
 Quote Quote  Modify Modify
|
I held the belief that (for analogy, inform me if the analogy doesn't apply) if g(x) = (x-1)/(x-1), then g would not have a value at x = 1.
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Radically Constant
« Reply #5 on: Aug 2nd, 2010, 7:24am » |
 Quote Quote  Modify Modify
|
I'm not really sure.
If one insists sqrt has to be real, then you can't calculate the values of the function for x < 1; but if you don't insist on that and allow complex values for sqrt then the overall function exists everywhere and is real for every x.
|
| « Last Edit: Aug 2nd, 2010, 7:25am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Radically Constant
« Reply #6 on: Aug 2nd, 2010, 7:37am » |
 Quote Quote  Modify Modify
|
I believe the intention is that the square root is meant to be real.
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2874
|
 |
Re: Radically Constant
« Reply #7 on: Aug 2nd, 2010, 8:59am » |
 Quote Quote  Modify Modify
|
on Aug 2nd, 2010, 7:12am, 0.999... wrote:| I held the belief that (for analogy, inform me if the analogy doesn't apply) if g(x) = (x-1)/(x-1), then g would not have a value at x = 1. |
|
In your example, g has a well-defined value everywhere except x=1, and the same well-defined limit as x tends to 1 from both directions, so there is a unique, well-defined function, everywhere continuous, that is equal to g whenever x is not 1, where g is not necessarily defined, so, by including continuity as a condition on g, you can treat it as having a value at x=1.
My default interpretation would be to say that g has a value at x=1 and only pay attention to the distinction between the continuous version of g, and the, mostly discontinuous, family of well-defined functions that are equal except at x=1, only paying attention to that distinction if it's brought up by context.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register