 Author
Author |
Topic: Numerically Attractive (Read 1351 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Numerically Attractive
« on: May 26th, 2010, 6:07pm » |
 Quote Quote  Modify Modify
|
Consider a 4-digit number whose digits are not all equal. With these four digits form the larget possible number M and the smallest possible number m. Calculate M - m and replace the original 4-digit number with the result. Prove that repeating this procedure always arrives at the same number.
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Noke Lieu
Uberpuzzler
    

pen... paper... let's go! (and bit of plastic)

Gender: 
Posts: 1884
|
 |
Re: Numerically Attractive
« Reply #1 on: May 26th, 2010, 8:08pm » |
 Quote Quote  Modify Modify
|
I'm assuming that there's a missing eventually int here.
Given a > b > c > d
M=(1000a+100b+10c+d)
m= (1000d + 100c +10b +a)
M-m= 9(111a + 10b - 10c - 111d) =
9(100(a-d)+10(a+b-d-c)+(a+d)) = n
9(100(a+d)+10(a+b-d-c)+(a-d)) = N
N-n = 9(200d + d)
hang on, that doesn't work... 
|
| « Last Edit: May 26th, 2010, 8:08pm by Noke Lieu » |
 IP Logged IP Logged |
a shade of wit and the art of farce.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Numerically Attractive
« Reply #2 on: May 27th, 2010, 2:26am » |
 Quote Quote  Modify Modify
|
on May 26th, 2010, 8:08pm, Noke Lieu wrote:| I'm assuming that there's a missing eventually int here. |
|
To give you an idea how long it takes, here's a table that shows how many numbers take a given number of steps:
#steps #nums
0 1
1 356
2 519
3 2124
4 1124
5 1379
6 1508
7 1980
>7 0
[edit]If you don't allow numbers to start with 0, you have to exclude multiples of 1000 as well as multiples of 1111 (you get 0 in both cases, rather than the intended 'attractor'). And the table becomes:
#steps #nums
0 1
1 287
2 600
3 813
4 380
5 396
6 1296
7 1365
8 1341
9 785
10 1235
11 483
>11 0
[/edit]
[edit2]Oh, and of course this assumes you add extra zeros when M-m < 1000. Otherwise it becomes more complicated still.[/edit2]
|
| « Last Edit: May 27th, 2010, 3:17am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Numerically Attractive
« Reply #3 on: Aug 1st, 2010, 7:06am » |
 Quote Quote  Modify Modify
|
Let
M = abcd
and
m = dcba
where
a 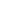 b b
c 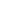 d d
a > d
There are two cases to consider:
1) b > c
Subtracting,
a b c d
- d c b a
---------------------------------------------
[a - d] [b - 1 - c] [10 + c - 1 - b] [10 + d - a]
---------------------------------------------
The 1st and 4th digits of the result sum to 10
and
The 2nd and 3rd digits of the result sum to 8
2) b = c
Subtracting,
a b c d
- d c b a
---------------------------------------------
[a - 1 - d] [10 + b - 1 - c] [10 + c - 1 - b] [10 + d - a]
---------------------------------------------
In this case,
the 1st and 4th digits of the result sum to 9
and
the 2nd and 3rd digits of the result sum to 18
Case 1 gives rise to 25 numbers of the required form
and
Case 2 to 5 such numbers, where order of digits is not important for forming the next M and m.
These all quickly converge on the numerical attractor, 6174.
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register