 Author
Author |
Topic: Cyclic quadrilateral and orthogonal circle (Read 4232 times) |
|
O09
Newbie


Posts: 6
|
 |
Cyclic quadrilateral and orthogonal circle
« on: Oct 18th, 2009, 9:59pm » |
 Quote Quote  Modify Modify
|
Let ABCD be a cyclic quadrilateral with no parallel sides. Let AB and CD intersect at M and let AD and BC intersect at N. Prove that the circle with MN as diameter is orthogonal to the circle through ABCD.
|
|
 IP Logged IP Logged |
|
|
|
humbern
Newbie


Posts: 5
|
I've been playing with this far too long, with no joy.
Cyclic quads, ortho circs, harmonic division.
Can the author or a kind soul help out?
...And explain how this is "easy"?
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Cyclic quadrilateral and orthogonal circle
« Reply #2 on: Mar 24th, 2010, 3:09am » |
 Quote Quote  Modify Modify
|
Nice picture, what software did you use for that?
Anyway, I think by now we can safely assume this problem isn't easy. I'll move it to medium for now.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
humbern
Newbie


Posts: 5
|
 |
Re: Cyclic quadrilateral and orthogonal circle
« Reply #3 on: Mar 24th, 2010, 8:12am » |
 Quote Quote  Modify Modify
|
The software is Cinderella. The frustration is mine. Any ideas out there?
|
|
 IP Logged IP Logged |
|
|
|
Ronno
Junior Member
 

Gender: 
Posts: 140
|
 |
Re: Cyclic quadrilateral and orthogonal circle
« Reply #4 on: Apr 1st, 2010, 6:10am » |
 Quote Quote  Modify Modify
|
Yes I agree, this should be at least in medium. Having solved this before I'll give a hint.
In your diagram, notice that AC, BD and LT are concurrent
|
| « Last Edit: Apr 1st, 2010, 6:10am by Ronno » |
 IP Logged IP Logged |
Sarchasm: The gulf between the author of sarcastic wit and the person who doesn't get it..
|
|
|
humbern
Newbie


Posts: 5
|
 |
Re: Cyclic quadrilateral and orthogonal circle
« Reply #5 on: Apr 2nd, 2010, 2:17pm » |
 Quote Quote  Modify Modify
|
Thank you!
And . . . cool!
And . . . I have to think about this....
|
|
 IP Logged IP Logged |
|
|
|
malchar
Junior Member
 



Gender: 
Posts: 54
|
 |
Re: Cyclic quadrilateral and orthogonal circle
« Reply #6 on: Apr 2nd, 2010, 10:24pm » |
 Quote Quote  Modify Modify
|
What does it mean for circles to be orthogonal?
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Cyclic quadrilateral and orthogonal circle
« Reply #7 on: Apr 3rd, 2010, 3:11am » |
 Quote Quote  Modify Modify
|
on Apr 2nd, 2010, 10:24pm, malchar wrote:| What does it mean for circles to be orthogonal? |
|
It means that at the points where the circles cross, if you draw the tangents of the circles, those tangents are at 90 degree angle.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
humbern
Newbie


Posts: 5
|
 |
Re: Cyclic quadrilateral and orthogonal circle
« Reply #8 on: May 17th, 2010, 9:26am » |
 Quote Quote  Modify Modify
|
Somebody please post an answer. This is killing me.
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: Cyclic quadrilateral and orthogonal circle
« Reply #9 on: May 19th, 2010, 5:44am » |
 Quote Quote  Modify Modify
|
I also don't know the answer.
But it seems that the line MN is the polar of the intersection of AC and BD.
http://mathworld.wolfram.com/InversePoints.html
I don't know if that helps.
|
|
 IP Logged IP Logged |
|
|
|
Noke Lieu
Uberpuzzler
    

pen... paper... let's go! (and bit of plastic)

Gender: 
Posts: 1884
|
 |
Re: Cyclic quadrilateral and orthogonal circle 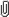 orthcir.jpg orthcir.jpg
« Reply #11 on: May 23rd, 2010, 9:04pm » |
 Quote Quote  Modify Modify
|
... I struggle to check if I've got the cart before the horse, but taking a simplistic approach...
MTN is 90o
Point Y is where TN bisects circle ABCD
extend PT throught to the other side of the circle ABCD to point Z
That also gives TYZ as 90o
From there, angle MT(red circle tangent)= angle TZY... and so on.
(did have a diag, but can't seem to save it, sorry)
actually, I reckon I've stuffed up- This only follows if they're orthongonal.
|
| « Last Edit: May 24th, 2010, 5:03pm by Noke Lieu » |
 IP Logged IP Logged |

a shade of wit and the art of farce.
|
|
|
Immanuel_Bonfils
Junior Member
 

Posts: 114
|
 |
Re: Cyclic quadrilateral and orthogonal circle
« Reply #12 on: May 27th, 2010, 9:38pm » |
 Quote Quote  Modify Modify
|
Grimbal went close!
Indeed, line MN is polar of the intersection of AC and BD, let's call it X..
But the best is that the line MK is polar of N wrt circumcircle O1, of the quadrilateral ABCD, so MK is perpendicular to ON, let's say at Y, and Y is a point of the circle O2 with diameter MN.
So from the condition for Y to be the inverse (or the image) of N wrt O1 we have
|OY|.|ON| = |OT|2, where T is a point of O1 and |OT| is his radius.
But |OY|.|ON| = |OT|2 is also the power of O wrt O2, so OT is the tangent to O2 taken from O . Done .
It's circle inverse geometry, but I think folks aren't much fan of, since I've post some time ago a problem in the subject http://www.ocf.berkeley.edu/~wwu/cgi-bin/yabb/YaBB.cgi?board=riddles_med ium;action=display;num=1214764919 and nothing happened...
|
|
 IP Logged IP Logged |
|
|
|
humbern
Newbie


Posts: 5
|
 |
Re: Cyclic quadrilateral and orthogonal circle
« Reply #13 on: Jun 1st, 2010, 12:22pm » |
 Quote Quote  Modify Modify
|
Thank you so much! This is actually really thrilling, although I'm still trying to put your reasoning into the simplest possible terms, given my purely recreational background. But I see the through-line. You might be interested to know that the forward to the recent biography of Donald Coxeter was written by Douglas Hofstadter (of Goedel, Escher, Bach fame), and he recalls his biggest aha! moment of math education as being taught about circle inversion. I'll be thinking about your "nothing happened" problem as soon as I can explain this current one to my co-workers, who have watched me banging my head...
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register