 Author
Author |
Topic: Form a Square (Read 853 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Form a Square
« on: Jan 8th, 2010, 6:17am » |
 Quote Quote  Modify Modify
|
Two players take turns marking the vertices of an infinite Cartesian grid. The winner is the first one to form a square using any of the marked vertices. Does either player have a forced wiin? (Dunno how hard it is.)
|
| « Last Edit: Jan 8th, 2010, 6:26am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Form a Square
« Reply #1 on: Jan 8th, 2010, 7:38am » |
 Quote Quote  Modify Modify
|
| hidden: | Neither player can force a win.
- it is only possible to win by placing the forth corner of a square.
- therefore it is only possible to lose by placing the third corner of a square, i.e. forming an isosceles right triangle.
- at any point in the game only a finite number of isosceles right triangles can be formed: at most 3n(n-1) where n is the number of points already placed.
- therefore at any point in the game there are only a finite number of losing moves.
- there are always an infinite number of possible moves.
- therefore it is always possible to choose a non-losing move.
Q.E.D.
|
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Form a Square
« Reply #2 on: Jan 8th, 2010, 7:54am » |
 Quote Quote  Modify Modify
|
What if they have their own colours, have to form a square of only their colour, and can't recolour any of the other's vertices
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Form a Square
« Reply #3 on: Jan 8th, 2010, 8:09am » |
 Quote Quote  Modify Modify
|
Then there's an easy forced win for the first player:
1. (0,0) any
2. (2x,0) any
3. (x,x)+ (x,-x)
4. (x,0)++ any
5. (0,x) OR (0,2x) whichever is free
I think moves 2 and 3 can be rotated/scaled/mirrored in response to the second player's free moves to always allow the first player to set up a split on move 4 and win on move 5.
Edit: hmm, what if the second player takes (x,x) (or equivalently (x,-x)) on the second move? I'm pretty sure the first player can still set up a split in short order, but it may take one-or-two more moves.
Edit 2: in that case,
2. (2x,0) (x,x)
3. (0,2x)+ (2x,2x)
4. (0,-2x)++ any
5. (-2x,0) OR (2x,-2x) whichever is free
Edit 3: Missed a few more cases where player 2 could force a move by player 1 and take control. The following is, I believe, comprehensive.
Let the first moves of each player define a right-handed Cartesian coordinate system overlaying the original grid
1. (0,0) (1,0)
Next player 1 moves, and player 2 has a free move
2. (2,0) (x,y)
And here we split to four cases...
A) If (x,y) = (0,2) then
3. (2,-2)+ (0,-2)
4. (4,0)++ any
5. (4,-2) or (2,2)
B) If (x,y) = (2,2) then
3. (0,-2)+ (2,-2)
4. (-2,0)++ any
5. (-2,-2) or (0,2)
C) If (x,y) = (-2,2) or (-2,0) or (-1, 1) or (0,3) or (0,-2) or (3,-1) or (4,1)
3. (2,2)+ (0,2)
4. (4,0)++ any
5. (4,2) or (2,-2)
D) Otherwise
3. (0,2)+ (2,2)
4. (-2,0)++ any
5. (-2,2) or (0,-2)
Edit 4: formatting, two missed points for case C)
--SMQ
|
| « Last Edit: Jan 9th, 2010, 5:17am by SMQ » |
 IP Logged IP Logged |
--SMQ
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: Form a Square
« Reply #4 on: Jan 12th, 2010, 6:42am » |
 Quote Quote  Modify Modify
|
I would start with say (0,0), ( ,0) coordinate system to be more sure first opponent move would not interfere with mine whole number ones ... ,0) coordinate system to be more sure first opponent move would not interfere with mine whole number ones ...
Not so easy ... I get those cases ... (second opponent move not on the x axis defines positive y ... or we choose it on our third)
(0,0) ( ,0) (2,0) ,0) (2,0)
If (2,-2) is a third vertex of opponents square choose it for 3rd move, otherwise choose (0,-2).
Opponent responses to check by the other one. And we are not in check now.
If 2nd move of opponent was not (1,1) the fourth move (1,-1)++ is double check.
else (-2,0)++ is double check.
BTW: You can replace  by 10 if you prefere by 10 if you prefere 
|
| « Last Edit: Jan 12th, 2010, 7:48am by Hippo » |
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Form a Square
« Reply #5 on: Jan 12th, 2010, 7:16am » |
 Quote Quote  Modify Modify
|
I was interpreting "Cartesian grid" as "two-dimensional orthogonal lattice" in the problem statement, i.e. isomorphic to 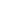 2. 2.
--SMQ
|
| « Last Edit: Jan 12th, 2010, 7:19am by SMQ » |
 IP Logged IP Logged |
--SMQ
|
|
|
Ant_Man
Newbie


Gender: 
Posts: 23
|
 |
Re: Form a Square
« Reply #6 on: Jan 19th, 2010, 1:05pm » |
 Quote Quote  Modify Modify
|
Hmmm. What if the winning square had to oriented with the grid? It seems like smq had player 1 winning by exploiting those diagonal squares to force player 2's moves and then win with a grid-oriented square (at least in case 1). I think player 1 can still guarantee a win, though it may take more moves.
|
| « Last Edit: Jan 19th, 2010, 1:32pm by Ant_Man » |
 IP Logged IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2874
|
 |
Re: Form a Square
« Reply #7 on: Jan 29th, 2010, 9:43am » |
 Quote Quote  Modify Modify
|
on Jan 19th, 2010, 1:05pm, Ant_Man wrote:| Hmmm. What if the winning square had to oriented with the grid? It seems like smq had player 1 winning by exploiting those diagonal squares to force player 2's moves and then win with a grid-oriented square (at least in case 1). I think player 1 can still guarantee a win, though it may take more moves. |
|
Unless I've missed something:
1 (0,0); (x,y)
with x,y non-zero
2 (n,n) with n>>x+y; (0,n) (determining axes)
3 (n,-n)!; any
if (2n,n), (2n,0), (2n,-n), (n,0), (0,-n), (-2n,n), (-2n,-2) are all free
4 (n,0)+; (0,-n)
5 (2n,0)++; any
6 whichever of (2n,n) and (2n,-n) is free
otherwise
4 (-n,n)+; (-n,-n)
5 (3n,n)+; (3n,-n)
6 (n,3n)++; any
7 whichever of (-n,3n), (3n,3n) is free
with y=0 (determining which axis is x and which y)
2 (2n,0) with n>>|x| (sign of the x-axis); (0,2n) or (2n,2n) (sign of the y-axis)
3 (n,0); any
if (0,n), (n,n) and (2n,n) are free
4 (n,n)++; any
5 whichever of (0,n) and (2n,n) is free
otherwise
4 (n,-n)++; any
5 whichever of (0,-n) and (2n,-n) is free
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Form a Square
« Reply #8 on: Jan 29th, 2010, 10:20am » |
 Quote Quote  Modify Modify
|
on Jan 29th, 2010, 9:43am, rmsgrey wrote:| 2 (n,n) with n>>x+y; (0,n) (determining axes) |
|
What if player 2 chooses to not to play on either axis again? You seem to be missing that branch.
Quote:
 at annotating your own move with ! at annotating your own move with !
--SMQ
|
| « Last Edit: Jan 29th, 2010, 10:23am by SMQ » |
 IP Logged IP Logged |
--SMQ
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2874
|
 |
Re: Form a Square
« Reply #9 on: Jan 30th, 2010, 1:15pm » |
 Quote Quote  Modify Modify
|
on Jan 29th, 2010, 10:20am, SMQ wrote:
What if player 2 chooses to not to play on either axis again? You seem to be missing that branch.
--SMQ |
|
If he doesn't play (0,n) or (n,0) then it's an easy forced win - defining the axes such that the last move was not below the x=y diagonal:
...
3 (n,0)+; (0,n)
4 (2n,0)+; (2n,n)
5 (n,-n)++; any
6 whichever of (0,-n) and (2n,-n) is free
In general, two points on the same orthogonal line, or on the same 45-degree diagonal, if unanswered, will allow that player to keep his opponent "in check" until they win - the reason for the two main lines is to keep player 2's blocking move on turn 2 from creating such a position and requiring player 1 to suspend development of his own position to prevent player 2 from winning - if player 2's first move is on one of the main diagonals, or on one of the axes, then playing the wrong line allows player 2 to take the initiative (sort of a reverse strategy stealing); otherwise, either line would work.
|
| « Last Edit: Jan 30th, 2010, 1:41pm by rmsgrey » |
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register