 Author
Author |
Topic: Smallest Equilateral Triangle (Read 576 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Smallest Equilateral Triangle
« on: Nov 28th, 2009, 2:51am » |
 Quote Quote  Modify Modify
|
Find the area of the smallest equilateral triangle inscribable in a right triangle of legs a and b.
|
| « Last Edit: Dec 3rd, 2009, 5:54am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Immanuel_Bonfils
Junior Member
 

Posts: 114
|
 |
Re: Smallest Equilateral Triangle
« Reply #1 on: Nov 30th, 2009, 6:39pm » |
 Quote Quote  Modify Modify
|
ABC is the right triangle and P P P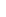 P P the inscribed equilateral with vetices respecively in AB, BC and CA, side length x. the inscribed equilateral with vetices respecively in AB, BC and CA, side length x.
Let 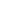 ABC = ABC =  (constant or known: sin (constant or known: sin  =b/ =b/ (a (a + b + b ) ) and ) ) and 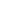 P P P P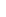 C= C= (variable or unknown). (variable or unknown).
Sinus law in triangle P BP BP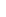 leads to leads to
x = a.sin  /(sin( /(sin( /3+ /3+ - - )+cos )+cos .sin .sin ) (*), ) (*),
that has a minimum for cot  =(sin =(sin +sin( +sin( /3- /3- ))/cos( ))/cos( /3- /3- )). )).
Substitution in (*) gives us x that multiplied by ( that multiplied by ( 3)/4 leads to the required area. 3)/4 leads to the required area.
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Smallest Equilateral Triangle
« Reply #2 on: Dec 1st, 2009, 2:49am » |
 Quote Quote  Modify Modify
|
I will bear that in mind, but I was looking for a simple formula f(a,b).
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Smallest Equilateral Triangle
« Reply #3 on: Dec 1st, 2009, 9:02am » |
 Quote Quote  Modify Modify
|
Place the right angle at the origin with leg a along the positive y-axis and leg b along the positive x-axis. Pick a point X = (x, 0) on side b. If we pick another point P anywhere on the triangle, there are two points Q and Q' which will form an equilateral triangle with X and P. The sets of Q and Q' over all P form images of the triangle rotated by +/-120o around point X. To find the inscribed equilateral triangle containing X we can find point Y = (0, y): the intersection of the image of the hypotenuse (rotated +120o) with leg a, i.e. the y-axis. With some algebra, we obtain y = [(b - x) 3]/2 - (b + x)(b 3]/2 - (b + x)(b 3 - a)/[2(b + a 3 - a)/[2(b + a 3)]. 3)].
We now seek to minimize XY =  (x2 + y2). Equivalently, and more simply, we can minimize XY2 = x2 + y2. Setting d/dx (x2 + y2) = 0 gives, following some more algebra, x2 + y2 = a2b2/(a2 + ab (x2 + y2). Equivalently, and more simply, we can minimize XY2 = x2 + y2. Setting d/dx (x2 + y2) = 0 gives, following some more algebra, x2 + y2 = a2b2/(a2 + ab 3 + b2). 3 + b2).
Finally, the area of the inscribed equilateral triangle = (XY2 3)/4 = [(x2 + y2) 3)/4 = [(x2 + y2) 3]/4, so the area of the minimal inscribed equilateral triangle is (a2b2 3]/4, so the area of the minimal inscribed equilateral triangle is (a2b2 3)/[4(a2 + ab 3)/[4(a2 + ab 3 + b2)]. 3 + b2)].
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Smallest Equilateral Triangle
« Reply #4 on: Dec 1st, 2009, 10:51am » |
 Quote Quote  Modify Modify
|
Excellent, SMQ, as always.
I will shortly post a solution that uses a neat little substitution to simplify matters. Perhaps even a diagram, but I am presently using Vista and most of my drawing software doesn't seem to want to work with it. Although Cabri doesn't seem very fussy.
|
| « Last Edit: Dec 1st, 2009, 10:53am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Smallest Equilateral Triangle
« Reply #5 on: Dec 26th, 2009, 2:24pm » |
 Quote Quote  Modify Modify
|
Sorry, no diagram.
But with a pencil and paper draw the right-angled triangle ABC, with AC as the hypotenuse.
Let AB = a and BC = b
Now draw the inscribed equilateral triangle DEF with D on AC, E on AB, and F on BC
Let BF = b1 and FC = b2
Let DE = EF = FD = s
Let angle EFB = 
Let angle DCF = 
Then angle FDC = 60 +  - - 
and
b = b1 + b2
= s*cos + [s*sin(60 + + [s*sin(60 +  - -  )/sin )/sin ] ]
Now letting r =  3 + b/a and p = 3 + b/a and p =  3b/a + 1 3b/a + 1
we obtain 1/s = (rsin + pcos + pcos )/2b )/2b
We seek 1/s to be a maximum when we differentiate wrt to 
and setting d(1/s)/d to zero we obtain to zero we obtain
tan = r/p and minimum value of s2 = a2b2/(a2 + = r/p and minimum value of s2 = a2b2/(a2 +  3ab + b2) 3ab + b2)
And required area =  3s2/4 = ( 3s2/4 = ( 3/4)a2b2/(a2 + 3/4)a2b2/(a2 +  3ab + b2) 3ab + b2)
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register