wu :: forums « wu :: forums - sum phi(n)/(2^n - 1) » Welcome, Guest. Please Login or Register. Nov 24th, 2024, 8:50pm

RIDDLES SITE WRITE MATH! Home Help Search Members Login Register

wu :: forums    riddles    medium (Moderators: SMQ, ThudnBlunder, Grimbal, towr, Eigenray, william wu, Icarus)    sum phi(n)/(2^n - 1) « Previous topic | Next topic » Pages: 1  Reply Notify of replies Send Topic Print    Author  Topic: sum phi(n)/(2^n - 1)  (Read 743 times) Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 sum phi(n)/(2^n - 1)   « on: Sep 9th, 2009, 9:23pm » Quote Modify Evaluate: 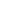n=1  (n)/(2n-1) IP Logged william wu wu::riddles Administrator     Gender: Posts: 1291 Re: sum phi(n)/(2^n - 1)   « Reply #1 on: Sep 13th, 2009, 2:43pm » Quote Modify Here is an upper bound that matches numerical calculation of the limit (thanks Eigenray):   hidden:   We first prove the following inequality: n/2n phi(n)/(2^n - 1) for n > 1. By rearranging, the inequality we wish to show can be rewritten as 1 - (1/2)^n phi(n)/n. This holds since   phi(n)/n   = p|n (1-1/p) <= 1-1/n <= 1 - (1/2)^n where the first inequality holds since n>1, and the second inequality holds since n <= 2^n.     Thus, applying this inequality to every term of our series except the first term, we have   n=1 to  phi(n) / (2^n - 1) <= 1 + n=2 to  n/2n = 1 + -1/2 + n=1 to  n/2n   = 2.5   In the last equality, the sum n/2^n can be evaluated by using the trick of differentiating the geometric series x^n = 1/(1-x) when |x|<1. In this way, we can show that n=1 to n x^n = x/(1-x)^2, which evaluates to 2 when x = 1/2.   « Last Edit: Sep 18th, 2009, 5:43am by william wu » IP Logged [ wu ] : http://wuriddles.com / http://forums.wuriddles.com Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: sum phi(n)/(2^n - 1)   « Reply #2 on: Sep 13th, 2009, 5:41pm » Quote Modify The only way the upper bound could be sharp is if it were sharp term by term, which it isn't.  The upper bound you give is actually 1 - 1/2 + 2 = 2.5   Hint: I intentionally made the problem more difficult by making it 'easier', i.e., asking for less information. IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: sum phi(n)/(2^n - 1)   « Reply #3 on: Sep 21st, 2009, 2:04am » Quote Modify Here is the 'harder' (easier) version: if x > 1, evaluate: (n)/(xn-1) IP Logged Pages: 1  Reply Notify of replies Send Topic Print Forum Jump: ----------------------------- riddles -----------------------------  - easy => medium   - hard   - what am i   - what happened   - microsoft   - cs   - putnam exam (pure math)   - suggestions, help, and FAQ   - general problem-solving / chatting / whatever ----------------------------- general -----------------------------  - guestbook   - truth   - complex analysis   - wanted   - psychology   - chinese « Previous topic | Next topic »

Powered by YaBB 1 Gold - SP 1.4!
Forum software copyright © 2000-2004 Yet another Bulletin Board