 Author
Author |
Topic: Never perfect square polynomial (Read 1658 times) |
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Never perfect square polynomial
« on: Sep 1st, 2009, 9:24am » |
 Quote Quote  Modify Modify
|
Show that there is a permutation ai (i = 1 to 13) of {1,2,..., 13} such that the polynomial
P(x) = Sum ai xi-1
is never a perfect square for any integral value of x.
In fact show that there are at least 7! such permutations (hopefully this one is true).
|
|
 IP Logged IP Logged |
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Never perfect square polynomial
« Reply #1 on: Sep 2nd, 2009, 12:16pm » |
 Quote Quote  Modify Modify
|
Cute! I should probably have seen further towards the solution than I did
right away, but at least this much I spotted: P won't be a square if it's
near a square.
So I looked to see which degree-12 polynomials are squares (and guessed
they should probably be monic); knowing P is a square, you can compute
half its coefficients from the other half, so I let the one half of the
coefficients range over {2,3,...,13} and computed the other half from
them. I found that there were two polynomials which differ by a constant
from a perfect square and for which the coefficients are {1,2,...,13}:
x^12+2*x^11+3*x^10+4*x^9+5*x^8+6*x^7+13*x^6+12*x^5+11*x^4+10*x^3+9*x^2+8 *x+7
x^12+2*x^11+3*x^10+4*x^9+5*x^8+6*x^7+12*x^6+11*x^5+10*x^4+9*x^3+8*x^2+7* x+13
The first is (x^6+x^5+x^4+x^3+x^2+x+4)^2 - 9 and the second is
(x^6+x^5+x^4+x^3+x^2+x+7/2)^2 + 3/4 . Of course it is possible for
(square)-9 or (square)+3 to be an integer square but that requires
that our polynomials equal 0 or 1 respectively, and as it turn out
those don't even happen for any REAL x.
The part I should have remembered but didn't is that (1+x+x^2+x^3...)^2
has among its coefficients the first few positive integers, and that
gives half the battle. With hindsight we now compute
(x^n + x^(n-1) + ... + x^2 + x + c/2)^2 =
x^(2n) + 2 x^(2n-1) + ... + n x^(n+1)
+ (n-1 + c) x^n + ... + (1 + c) x^2 + c x
+ c^2/4
so if we choose c=n+1 we have all the coefficients up to 2n+1 except
2n+1 itself, and have (n+1)^2/4 as the constant term; while if we choose
c=n+2 we have all the coefficients except n+1, and have (n+2)^2/4
as the constant term. So this gives us two nice polynomials
P = x^(2n) + ... + (2n)x^n + ... + (n+1) x + (2n+1) =
(x^n + x^(n-1) + ... + x^2 + x + (n+1)/2)^2 + (2n+1)-(n+1)^2/4
(i.e. P(x) = P0(x)^2 - (n^2-6n-3)/4 )
and
Q = x^(2n) + ... + (2n+1)x^n + ... + (n+2) x + (n+1) =
(x^n + x^(n-1) + ... + x^2 + x + (n+2)/2)^2 + (n+1)-(n+2)^2/4
(i.e. Q(x) = Q0(x)^2 - n^2/4 )
If for some integer x, P(x) is a square N^2, then we have an equation
among integers that (2N)^2 - (2P0(x))^2 = - (n^2-6n-3) ; for any fixed
value of n there are only finitely many ways to express -(n^2-6n-3) as
a difference of two squares (it's the same as the number of ways to
express -n^2+6n+3 as a product of two integers of the same parity),
and so we need only check to see whether the polynomial 2P0(x) can
achieve any of these values for integer values of x. I checked out
the values of n up to 200; the only times this happens were for
x=0, x=1, and x=-1, and for each of these, it is easy to find the values
of n for which P( x0 )^2 - (n^2-6n-3)/4 is a perfect square: only
n=3,4,12,14,24,... will do. So for most values of n (including your
original n=6) the polynomial P(x) is never a square for any integer x.
In exactly the same way if Q(x)=N^2 then we would have an integer equation
(2N)^2 - (2P0(x))^2 = - n^2
and that can happen for at most finitely many x. Again, a check through
small values of n showed that this can happen but (for these n)
only for x=0 or x=-1 or x=+1; and for these values we can
predict the values of n that will work (e.g. x=1 happens for
n=24, 840, 28560,... : we solve a Pell equation). Again, for most
(even) values of n, Q(x) will not be square for any integer x.
So you could have asked your question about the coefficients {1,2,3,4,5}
and gotten the same answer, but I guess that would have been too easy.
And similarly you could have used {1,2,3,...,21} but that would
have discouraged anyone from trying anything!
Nice problem!
I'll let someone else take the second part!
|
| « Last Edit: Sep 2nd, 2009, 12:19pm by Michael Dagg » |
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Re: Never perfect square polynomial
« Reply #2 on: Sep 3rd, 2009, 9:23am » |
 Quote Quote  Modify Modify
|
Interesting approach. I had a different approach altogether!
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Never perfect square polynomial
« Reply #3 on: Sep 3rd, 2009, 3:08pm » |
 Quote Quote  Modify Modify
|
Let's work mod 4 (since this approach doesn't work mod 3). That is, we take a linear combination of the functions x 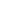 xk, with 0 xk, with 0  k < 13, using coefficients 1 k < 13, using coefficients 1  c c  13, such that the result takes on only the values {2,3} mod 4. 13, such that the result takes on only the values {2,3} mod 4.
There are only 4 distinct functions, represented by their values on (0,1,2,3) as:
(1,1,1,1) x 1
(0,1,2,3) x 1
(0,1,0,1) x 6
(0,1,0,3) x 5,
and our coefficients are chosen from the multiset C = { 03, 14, 23, 33 }. Thus we need to pick a,b  C, and a submultiset S C, and a submultiset S 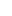 C' = C-{a,b} of size 6, such that the entries of C' = C-{a,b} of size 6, such that the entries of
a.(1,1,1,1) + b.(0,1,2,3) + |S|.(0,1,0,1) + (3-|S|-a-b).(0,1,0,3)
consist only of 2 and 3. From the first entry, a is 2 or 3, and from the third entry b is 0 or 2. Taking, say, a=b=2, say, the second and fourth entries become
|S| + (-1-|S|) = -1, and
|S| - (-1-|S|) = 2|S|+1,
so it is enough to find a subset of C'=C-{2,2} of size 6 with an odd sum, say S = { 03, 13 }, leaving C'-S = { 11, 21, 33 }. Lifting this back to 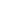 , one solution is , one solution is
2 + 6*x + 4*x2 + x3 + 8*x4 + 10*x5 + 12*x6 + 3*x7 + 5*x8 + 7*x9 + 9*x10 + 11*x11 + 13*x12
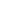 ( 2, 2, 0, 1, 0, 2, 0, 3, 1, 3, 1, 3, 1 ), ( 2, 2, 0, 1, 0, 2, 0, 3, 1, 3, 1, 3, 1 ),
with the underlined numbers representing elements of S.
There are many choices involved here. The pair (a,b) mod 4 can be chosen in 4 ways : a = 2,3; b = 0,2. Then we pick a subset S of C' of size 6 whose sum has the opposite parity of a, and then of course there are choices in lifting to 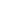 . In particular, given any solution, we get 5!*6! just by permuting the coefficients of the xk, with k in {2,4,6,8,10,12} and {3,5,7,9,11}. . In particular, given any solution, we get 5!*6! just by permuting the coefficients of the xk, with k in {2,4,6,8,10,12} and {3,5,7,9,11}.
|
|
 IP Logged IP Logged |
|
|
|
jpk2009
Junior Member
 

Gender: 
Posts: 60
|
 |
Re: Never perfect square polynomial
« Reply #4 on: Oct 4th, 2009, 7:28pm » |
 Quote Quote  Modify Modify
|
It is hard to get a grip on this. Aren't there lots of polynomials likes these just based on the coefficients and so you have to some how capture a general form for the solution? So if the set {1,2,3,4,5} generates some subset then it should be identical up to that subset. Kind of confusing....
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register