Author |
Topic: f(f(n)) not equal to n+3 (Read 590 times) |
|
Aryabhatta
Uberpuzzler
Gender: 
Posts: 1321
|
 |
f(f(n)) not equal to n+3
« on: Apr 1st, 2009, 10:37am » |
 Quote  Modify
|
let f: N -> N (N = Natural numbers = {1,2,3,....})
(i.e f is a function from the set of natural numbers to the set of natural numbers)
Show that there is some n such that
f(f(n)) is not equal to n+3.
|
|
 IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: f(f(n)) not equal to n+3
« Reply #1 on: Apr 1st, 2009, 11:58am » |
Quote Modify
|
Neat:
Consider the chains:
[1, x, 4, x+3, 7, x+6, 10, ... ]
[2, y, 5, y+3, 8, y+6, 11, ... ]
[3, z, 6, z+3, 9, z+6, 12, ... ]
Each chain contains one whole congruence class mod 3, plus a tail of another, necessarily different because f(f(n)) = n+3 is injective implies f injective. So each chain intersects another chain. Moreover, if two chains intersect, one must be a prefix of the other, because of injectivity. So one chain must contain the other two, hence every natural number. But it only has two congruence classes!
You may like the following cute result:
Let f : 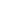  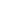be any function at all. Then no iterate of f (except possibly the first) can be equal to a quadratic polynomial.
This is due to Rice, Schweizer, Sklar [The American Mathematical Monthly, Vol. 87, No. 4 (Apr., 1980), pp. 252-263]. The proof is purely combinatorial.
|
|
IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
Gender:
Posts: 1321
|
|
Re: f(f(n)) not equal to n+3
« Reply #2 on: Apr 2nd, 2009, 8:47am » |
Quote Modify
|
on Apr 1st, 2009, 11:58am, Eigenray wrote:
You may like the following cute result:
Let f : 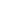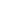be any function at all. Then no iterate of f (except possibly the first) can be equal to a quadratic polynomial.
This is due to Rice, Schweizer, Sklar [The American Mathematical Monthly, Vol. 87, No. 4 (Apr., 1980), pp. 252-263]. The proof is purely combinatorial. |
|
Interesting!
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print