 Author
Author |
Topic: Dividing a Ranch (Read 674 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Dividing a Ranch
« on: Feb 17th, 2009, 2:29am » |
 Quote Quote  Modify Modify
|
A rancher left a rather unusual will. Most of his estate went to his widow, but he stipulated that each of his four sons could take an exactly square plot of land if the dimensions fulfilled the following conditions. The area of Jeb's plot expressed in square miles must equal the length of Harry’s plot in miles, plus two. Similarly, Tony’s area must equal a side of Jeb’s area, plus two. Also, Harry’s area added to the length of Bob’s plot must equal two, and likewise Bob’s area plus the length of Tom’s plot must equal two.
What was the sons’ settlement?
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: Dividing a Ranch
« Reply #1 on: Feb 17th, 2009, 2:38am » |
 Quote Quote  Modify Modify
|
Easy, just solve the polynomial of degree 16. 
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Dividing a Ranch
« Reply #2 on: Feb 17th, 2009, 3:25am » |
 Quote Quote  Modify Modify
|
If all lengths have to be integer, then I don't see how there's a solution.
"Harry’s area added to the length of Bob’s plot must equal two"
h^2+b=2 -> h=b=1
"The area of Jeb's plot expressed in square miles must equal the length of Harry’s plot in miles, plus two"
j^2=h+2
j^2=3 -> !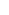 j j
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: Dividing a Ranch
« Reply #3 on: Feb 17th, 2009, 5:05am » |
 Quote Quote  Modify Modify
|
Well, I solved it numerically, then I googled the numerical value and found that
j = 2·cos(2pi/15) = 1.827090915
|
| « Last Edit: Feb 17th, 2009, 5:05am by Grimbal » |
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: Dividing a Ranch
« Reply #4 on: Feb 17th, 2009, 5:58am » |
 Quote Quote  Modify Modify
|
on Feb 17th, 2009, 5:05am, Grimbal wrote:Well, I solved it numerically, then I googled the numerical value and found that
j = 2·cos(2pi/15) = 1.827090915 |
|
Interesting! That implies that
t = 2*cos(1*pi/15)
j = 2*cos(2*pi/15)
h = 2*cos(4*pi/15)
b = 2*cos(7*pi/15)
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: Dividing a Ranch
« Reply #5 on: Feb 17th, 2009, 7:13am » |
 Quote Quote  Modify Modify
|
This solution actually suggests a solution method. 
| hidden: | The constraints can be summarized as follows:
h = j2 - 2
b = 2 - h2
t = 2 - b2
j = t2 - 2
If we make the substitution j = 2*cos(a), we find h = 4*cos2(a) - 2 = 2*[2*cos2(a) - 1] = 2*cos(2a). Continuing in this manner,
j = 2*cos(a)
h = 2*cos(2a)
b = -2*cos(4a)
t = -2*cos(8a)
j = 2*cos(16a)
Thus, we are looking for a solution to cos(a) = cos(16a). Restricting to 0 < a < pi (which is without loss of generality), the only interval in which j, h, b, and t are all positive is pi/8 < a < 3*pi/16.
The equation cos(a) = cos(16a) has only one solution in this interval. How to find it? Note that it is obvious that a = 2*pi/15 solves the equation, because then 16a = 15a + a = 2*pi + a. We happen to be lucky: pi/8 < 2*pi/15 < 3*pi/16.
Thus, the only solution is as follows:
j = 2*cos(2*pi/15) ~ 1.8271
h = 2*cos(4*pi/15) ~ 1.3383
b = -2*cos(8*pi/15) = 2*cos(7*pi/15) ~ 0.2091
t = -2*cos(16*pi/15) = 2*cos(pi/15) ~ 1.9563 |
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Dividing a Ranch
« Reply #6 on: Feb 18th, 2009, 4:39am » |
 Quote Quote  Modify Modify
|
That's the solution I had in mind, pex. 
on Feb 17th, 2009, 5:05am, Grimbal wrote:Well, I solved it numerically, then I googled the numerical value and found that
j = 2·cos(2pi/15) = 1.827090915 |
|
One can only marvel in awe at the many serpentine roads to mathematical truth. 
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register